How do you rotate the axes to transform the equation #4x^2-sqrt3xy+y^2=5# into a new equation with no xy term and then find the angle of rotation?
1 Answer
Here is a good reference on the topic Rotation of Conic Sections. Please see below.
Explanation:
The general Cartesian form for the equation of a conic section is:
Equation [9.4.6] in the reference gives us the angle of rotation:
In given equation,
Note: This is the angle of rotation that makes the
To find the un-rotated value for A, use equation [9.4.4a]:
We know that
To find the un-rotated value for C, use the equation [9.4.4c]:
Equation [9.4.4f] tells us that the constant is unchanged.
Here is the un-rotated equation:
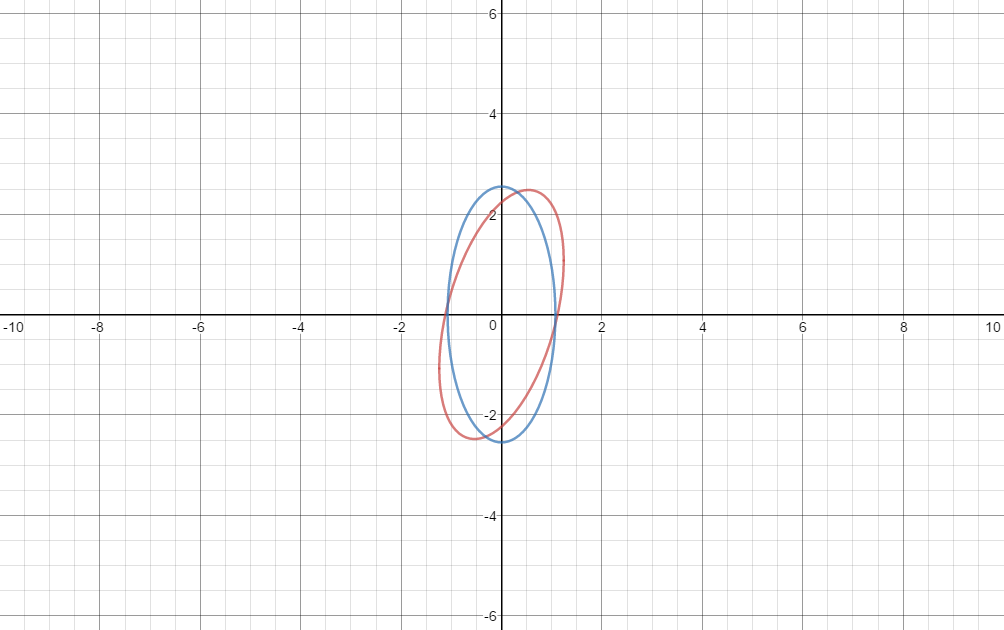
Here is a graph of both equations: