Question

How do you simplify `2/root6(81)`?

Answer 1

`(2root(3)(3))/(3)`

Explanation:

Step 1. It often helps to use a factor tree to determine the factors of 81.

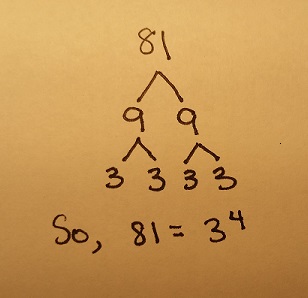
This gives us
`2/root(6)(3^4)`

Step 2. Rewrite the root as a fraction.
`2/((3^4)^(1/6))=2/(3^(4/6))=2/(3^(2/3))`

Step 3. Many Algebra teachers do not like roots in the denominator for some reason. So to fix this, you rationalize the denominator by multiplying the top and the bottom by `3^(1/3)`. Remember that this will cause you to add the exponents in with the same base in the denominator.
`2/(3^(2/3)) (xx3^(1/3))/(xx3^(1/3))=(2root(3)(3))/(3)`