How do you simplify #(3sqrt2+sqrt5)(sqrt2-3sqrt(5r))#?

Question

1535 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-13T18:08:10

#6 - 9sqrt(10r) + sqrt10 - 15sqrt(r)#

#(3sqrt2 + sqrt5)(sqrt2 - 3sqrt(5r))#

To simplify this, we will use the distributive method called FOIL:
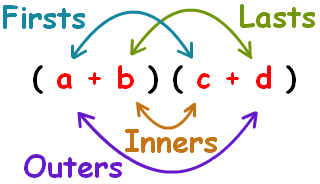
enter image source here

Following this image, we can multiply it out.

The #color(teal)("firsts")#:
#color(teal)(3sqrt2 * sqrt2) = 3sqrt4 = 3*2 = 6#

The #color(indigo)("outers")#:
#color(indigo)(3sqrt2 * -3sqrt(5r)) = 3 * -3 * sqrt(2 * 5r) = -9sqrt(10r)#

The #color(peru)"inners"#:
#color(peru)(sqrt5 * sqrt2) = sqrt(5*2) = sqrt10#

The #color(olivedrab)"lasts"#:
#color(olivedrab)(sqrt5 * -3sqrt(5r)) = -3sqrt(5*5r) = -3sqrt(25r) = -3*5sqrtr = -15sqrtr#

Combine them all together to get your answer:
#6 - 9sqrt(10r) + sqrt10 - 15sqrt(r)#

Hope this helps!