How do you simplify square root of 128 + the square root of 32?
4 Answers
Explanation:
Simplify:
Explanation:
Write both numbers as a product of prime numbers.
(unique factorisation ).
For example:
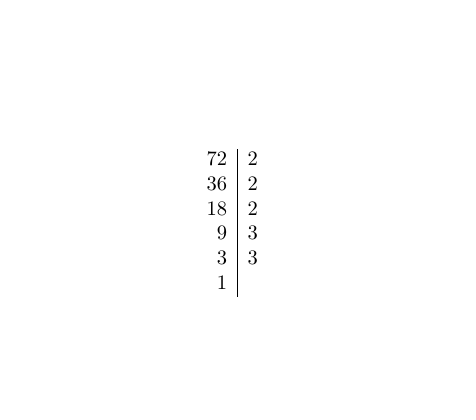
Explanation:
Given:
You are looking for squared values that you can 'extract' from the roots.
If you are ever not sure do a quick sketch of a prime factor tree to help: