How do you simplify the following expression?
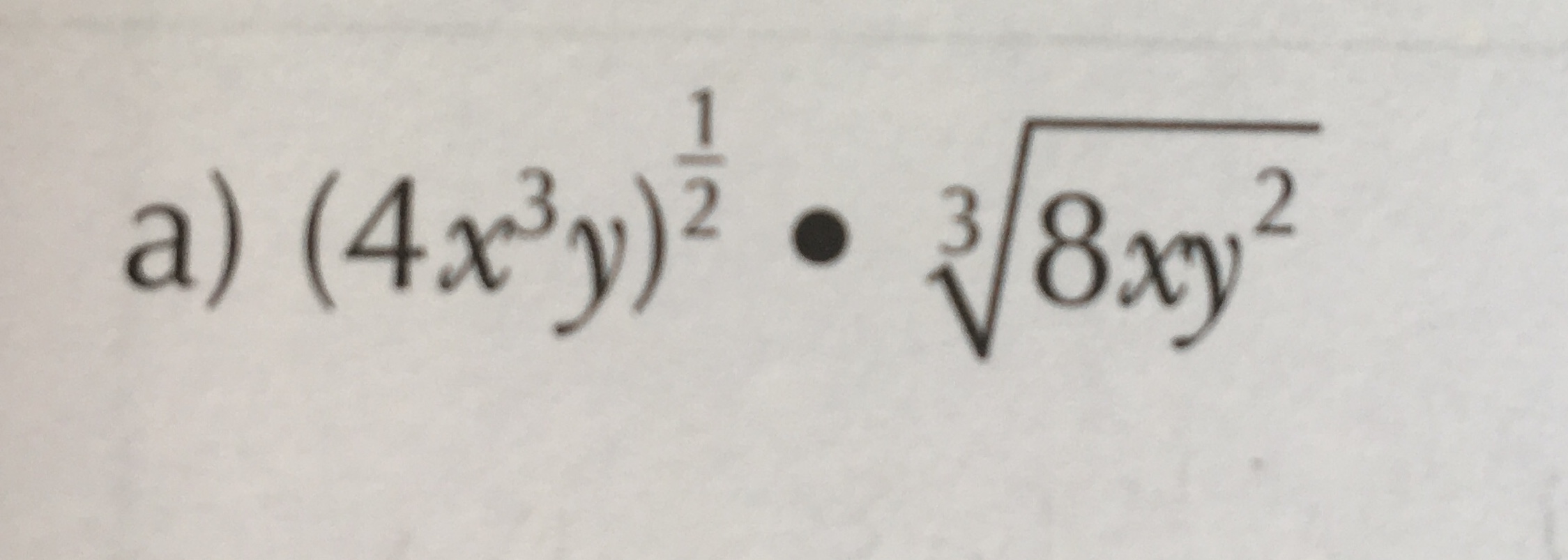
1 Answer
Mar 24, 2018
See below for the detailed steps.
The simplified form is
Explanation:
We can write a root as a fractional exponent or vice versa, so let's start here:
When we have an exponent on an expression in brackets we mutiply exponents:
Now
