How do you sipmify this ?
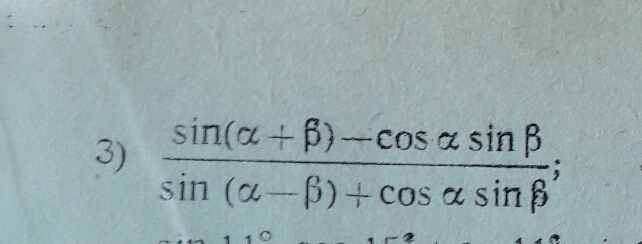 p
p
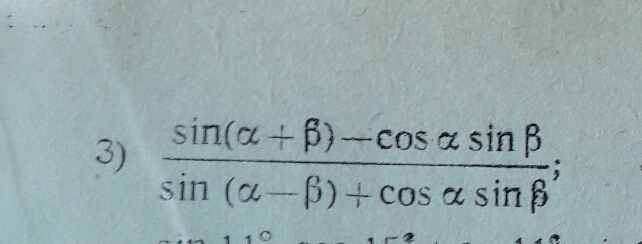 p
p
1 Answer
Apr 18, 2018
Explanation:
We want to simplify
(sin(a+b)-cos(a)sin(b))/(sin(a-b)+cos(a)sin(b))
The angle sum/difference identities
-
color(red)(sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
color(red)(=>sin(a+b)-cos(a)sin(b)=sin(a)cos(b) -
color(blue)(sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
color(blue)(=>sin(a-b)+cos(a)sin(b)=sin(a)cos(b)
Using the identities
(sin(a+b)-cos(a)sin(b))/(sin(a-b)+cos(a)sin(b))= (sin(a)cos(b))/(sin(a)cos(b))=1

