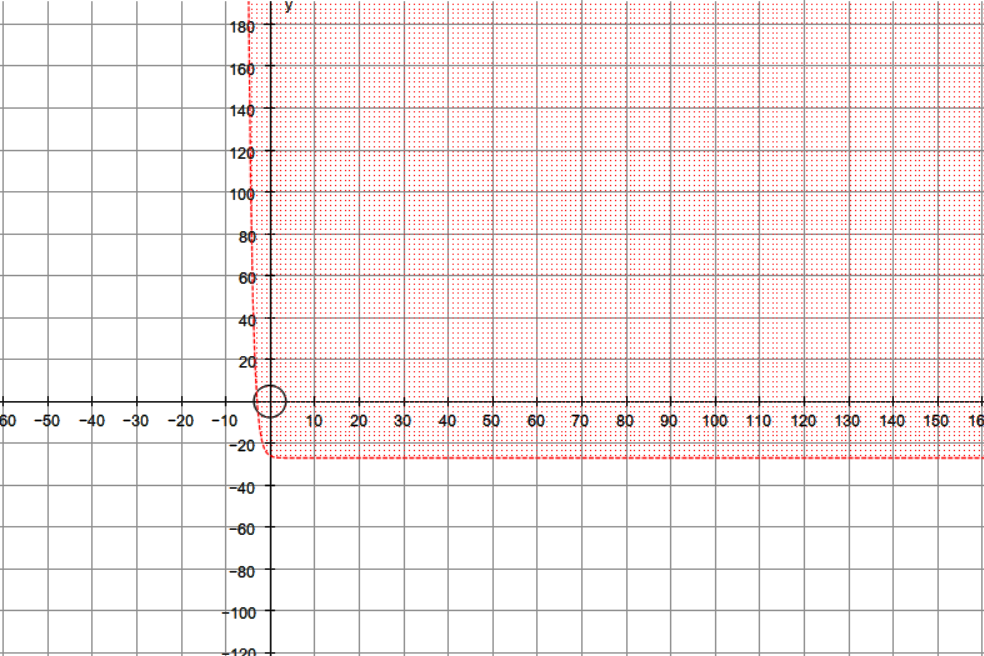
How do you solve #(1/3)^x-9<18# using a graph?
1 Answer
See below.
Explanation:
First Graph
This will give you the boundary between the included and excluded regions. Remember to use a dashed line, as this is a less than and not a less than or equal to inequality, so the line will not be an included region.
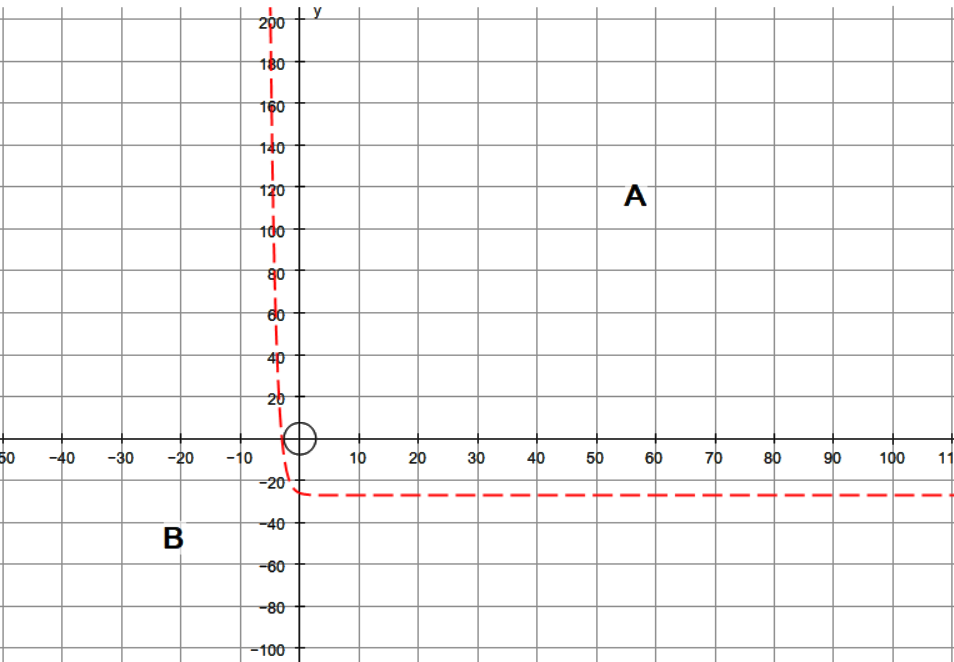
With the equation plotted, you will have to possible regions. These have been marked A and B on the graph. We need to test a pair of coordinates in each region to see which region satisfies the inequality.
Region A
coordinates
A is an included region.
Now we have found our region, we do not really need to test B. Will will check this just for clarity.
Region B
coordinates
B is an excluded region.
Shade region A