How do you solve #2X-3Y=21# and #5X+4Y=-5#?
2 Answers
Apr 13, 2018
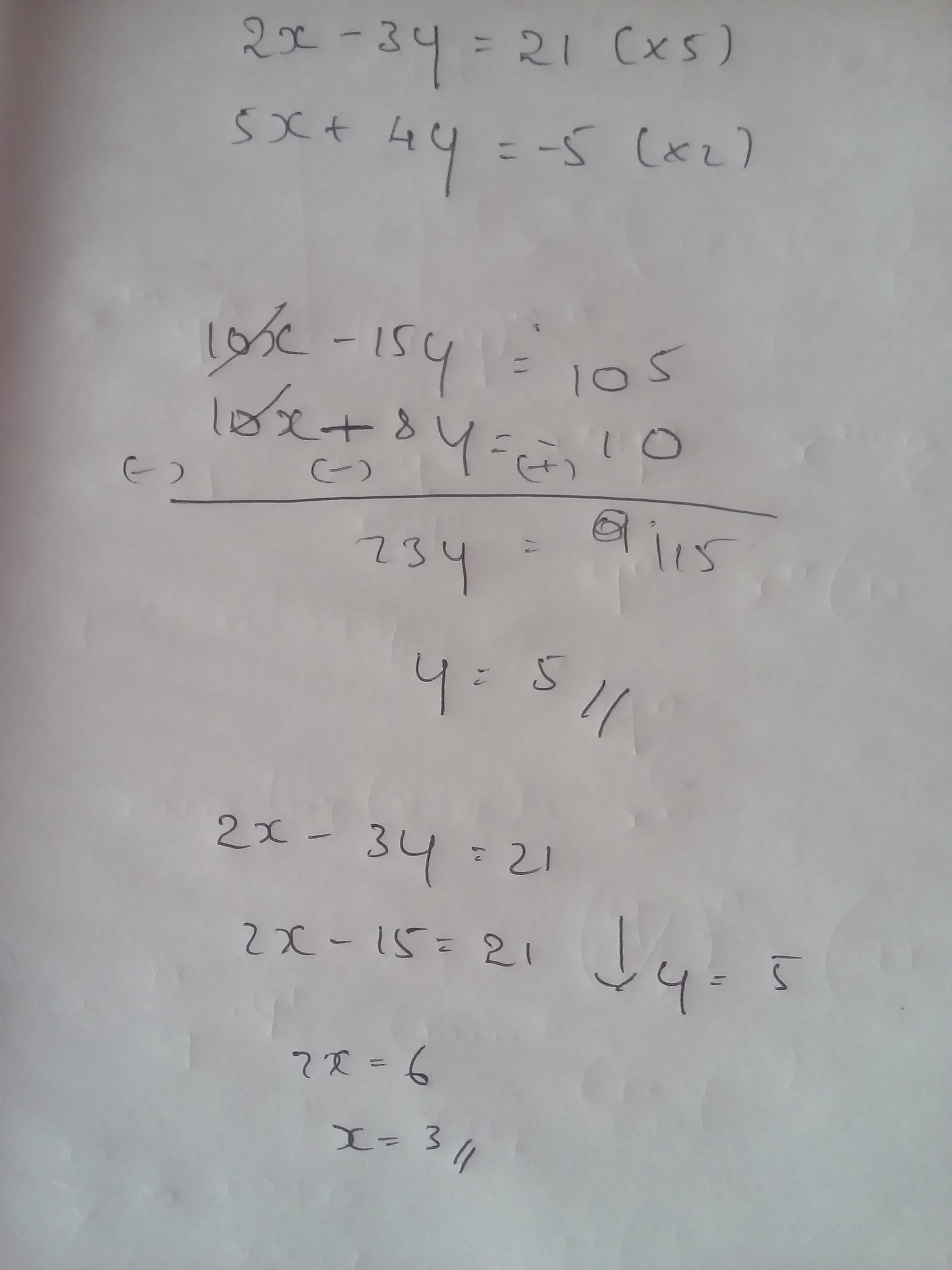
Apr 13, 2018
(3,-5)
Explanation:
I'm going to assume you are looking for the intersection of the two.
Lets start by solving both for y.
Now lets try seeing for what value of x, these two equations are equal (and therefore Y=Y)
And finally,
Now, lets find the value of y but inserting this x into either of the original equations!
Therefore, the answer is (X,Y)=(3,-5)
