How do you solve (2x - 7) ( x + 1) = 6x - 19(2x−7)(x+1)=6x−19?
2 Answers
Explanation:
Multiply out the Left hand side of the equation
Therefore
Collecting like terms on the left
Factorise
Explanation:
NOTE: This is a long answer.
Solve
FOIL the left-hand side.
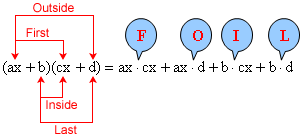 http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
Put the equation back together.
Subtract
Add
This is a quadratic equation,
Use the quadratic formula to solve for
Quadratic Formula