How do you solve #7/(x+5)+3/(x-5)=30/(x^2-25)# and check for extraneous solutions?
2 Answers
Feb 17, 2017
I got that it has no real solutions and only one extraneous.
Explanation:
Have a look:
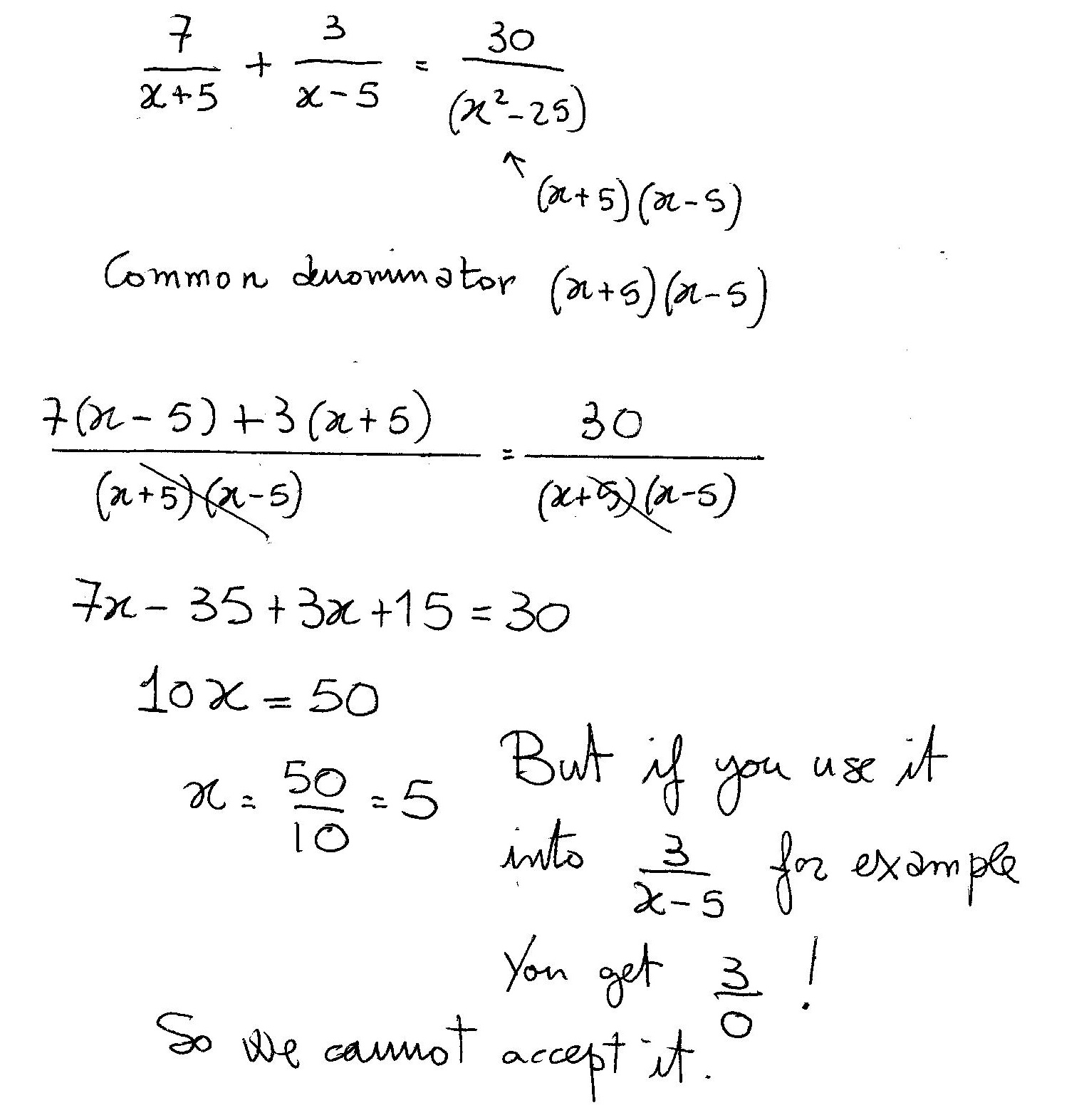
Feb 17, 2017
Note that
Explanation:
First we assert that
After that, we we multiply the first two terms by disguised
Together this adds up to:
And this is contrary to our first assertion.
Conclusion: there is no solution.


