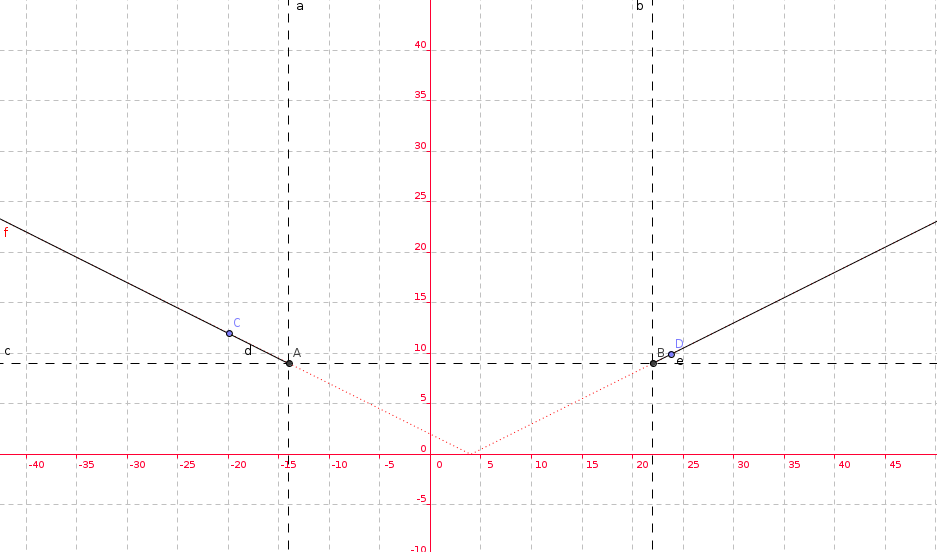
How do you solve and graph #abs((2p-8)/4)>=9#?

Question

2309 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-16T11:38:17

#p<=-14 or p>=22#

Let's consider that:

#|f(x)|>=a# is equivalent to

#f(x)<=-a or f(x)>=a#

Then

let's solve the equivalent form:

#(2p-8)/4<=-9 or (2p-8)/4>=9#

Let's multiply all terms by 4 to eliminate fractions:

#2p-8<=-36 or 2p-8>=36#

let's transfer -8 to the right side and divide all terms by 2:

#2p<=-28 or 2p>=44#

#p<=-14 or p>=22#

enter image source here