How do you solve and graph #abs(a-5)<3#?
1 Answer
Mar 16, 2017
Explanation:
The standard form for
#|x| < a # is.
#-a < x < a# This is used in the question here.
#rArr-3 < a-5 < 3# Isolate a in the centre interval by adding 5 to ALL 3 intervals.
#rArr-3+5 < acancel(-5)cancel(+5) < 3+5#
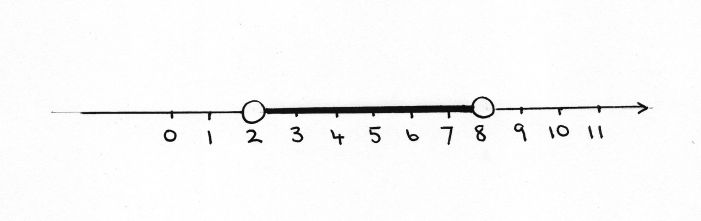
#rArr2 < a < 8larr" is the solution"#
To show the solution on a number line place
The solution is the values
#color(blue)"between"# 2 and 8 which is denoted by a heavy line drawn between the 2 open circles.