Question

How do you solve `e^ { 7x } = - 9e ^ { 2x }`?

Answer 1

Admin please delete this answer

Explanation:

I had some fundamental errors, then went to sleep, and others have answered in the mean time. Please delete my attempt.

Answer 2

No solution is possible (This is not a valid equation).
[Unless you allow `x=-oo` as a solution.]

Explanation:

`e^(7x)=e^7 * e^x`

`-9e^(2x)=(-9) * e^2 * e^x`

If `e^(7x)=-9e^(2x)`
then
`color(white)("XXX")e^7 * cancel(e^x) = (-9) * e^2 * cancel(e^x)`
`color(white)("XXXXXX")` with the provision that `e^x!=0`
`color(white)("XXXXXX")` which is only true as a limit of `xrarr-oo`

and
`color(white)("XXX")e^5 * cancel(e^2)=1 * cancel(e^2)`
`color(white)("XXXXXX")` which is obviously not true

Answer 3

See below.

Explanation:

Considering complex solutions and solving `e^(7z)=-9e^(2z)` instead, with `z = x + iy` we have then

`e^(7(x+iy))+9e^(2(x+iy))=0` or

`e^(7x) e^(i 7 y)+9e^(2x) e^(i 2y)=0` or

`e^(7x)(cos(7y)+isin(7y))+9e^(2x)(cos(2y)+isin(2y))=0` or

`{(e^(7x)cos(7y)+9e^(2x)cos(2y)=0),(e^(7x)sin(7y)+9e^(2x)sin(2y)=0):}`

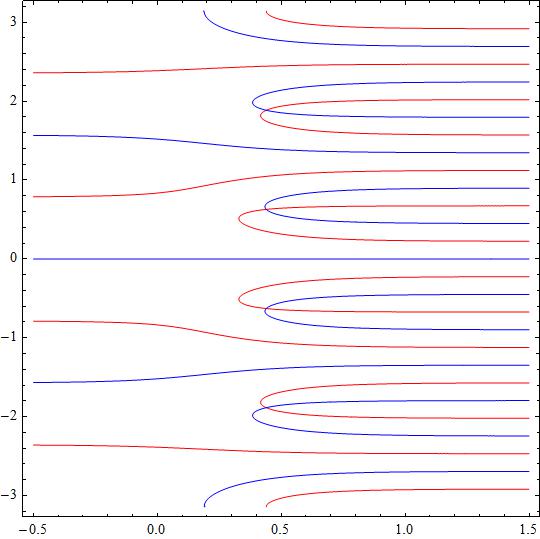
There are infinite complex solutions, as many as intersections of red and blue curves, as can be seen in the attached plot.

This plot was made for `-1/2 le x le 1.5` and `-pi le y le pi`

In red the trace for `e^(7x)cos(7y)+9e^(2x)cos(2y)=0`
in blue the trace for `e^(7x)sin(7y)+9e^(2x)sin(2y)=0`