Question

How do you solve for `a` is this equation `6(1-2a) + 9a < -9` ?

Answer 1

`color(red)(a > 5`

Explanation:

`" "`
Given inequality : `color(blue)(6(1-2a) + 9a < -9`

Use Distributive Property: `color(red)(a(b+-c)=ab +-ac`

`rArr 6-12a + 9a < -9`

Simplify by adding similar terms

`rArr 6-3a <-9`

Subtract `color(red)(6` from both sides of the inequality

`rArr 6-3a - color(red)(6) <-9- color(red)(6`

`rArr cancel 6-3a - color(red)(cancel 6) <-9- color(red)(6`

`rArr -3a <-15`

Multiply both sides of the inequality by `color(red)((-1)`

You must remember to reverse the inequality symbol.

If you divide or multiply by a negative value to simplify an equality, you must reverse the inequality symbol.

`rArr -3a * color(red)((-1)) <-15*color(red)((-1)`

`rArr 3a>15`

Divide both sides of the inequality by `color(red)(3`

`rArr (3a)/color(red)(3)>15/color(red)(3`

`rArr (cancel 3a)/color(red)(cancel 3)>cancel 15^color(red)(5)/color(red)(cancel 3`

Hence,

`color(blue)(a>5` is the final solution.

You can graph this solution as shown below:

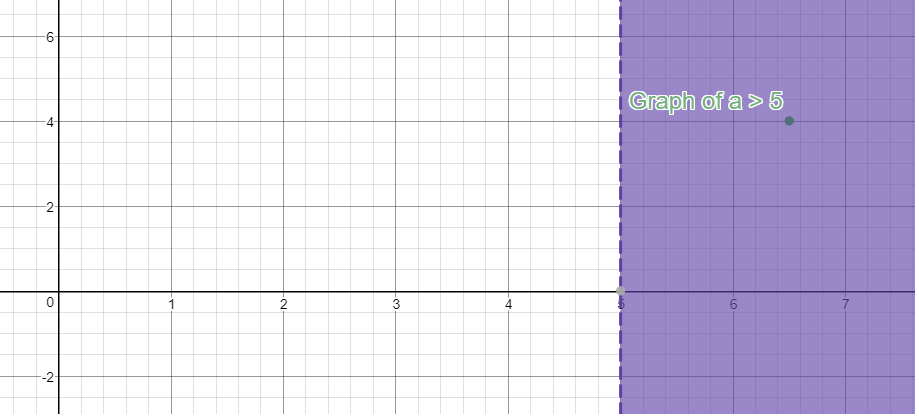
The dotted line indicates that `color(red)(a=5` is NOT a part of the final solution.

Hope it helps.