How do you solve #\frac { a + 12} { a - 10} = - \frac { 6} { 5}#?

1 Answer
smendyka
Jul 26, 2017

See a solution process below:

Explanation:

First, do a cross product or cross multiply the fractions:

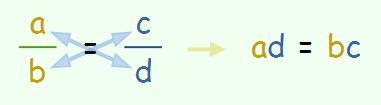
enter image source here

#(a + 12)/(a - 10) = (-6)/5#

#5(a + 12) = -6(a - 10)#

Next, expand the terms within parenthesis on each side of the equation by multiplying each term within the parenthesis by the term outside the parenthesis:

#color(red)(5)(a + 12) = color(blue)(-6)(a - 10)#

#(color(red)(5) * a) + (color(red)(5) * 12) = (color(blue)(-6) * a) - (color(blue)(-6) * 10)#

#5a + 60 = -6a - (-60)#

#5a + 60 = -6a + 60#

Then, subtract #color(red)(60)# and add #color(blue)(6a)# to each side of the equation to isolate the #a# term while keeping the equation balanced:

#color(blue)(6a) + 5a + 60 - color(red)(60) = color(blue)(6a) - 6a + 60 - color(red)(60)#

#11a + 0 = 0 + 0#

#11a = 0#

Now, divide each side of he equation by #color(red)(11)# to solve for #a# while keeping the equation balanced:

#(11a)/color(red)(11) = 0/color(red)(11)#

#(color(red)(cancel(color(black)(11)))a)/cancel(color(red)(11)) = 0#

#a = 0#

Related questions
Impact of this question
348 views around the world
You can reuse this answer
Creative Commons License