How do you solve #int_4^-2 |x-1|dx#?
1 Answer
Aug 10, 2016
Explanation:
Firstly, you evaluate rather than solve ;-)
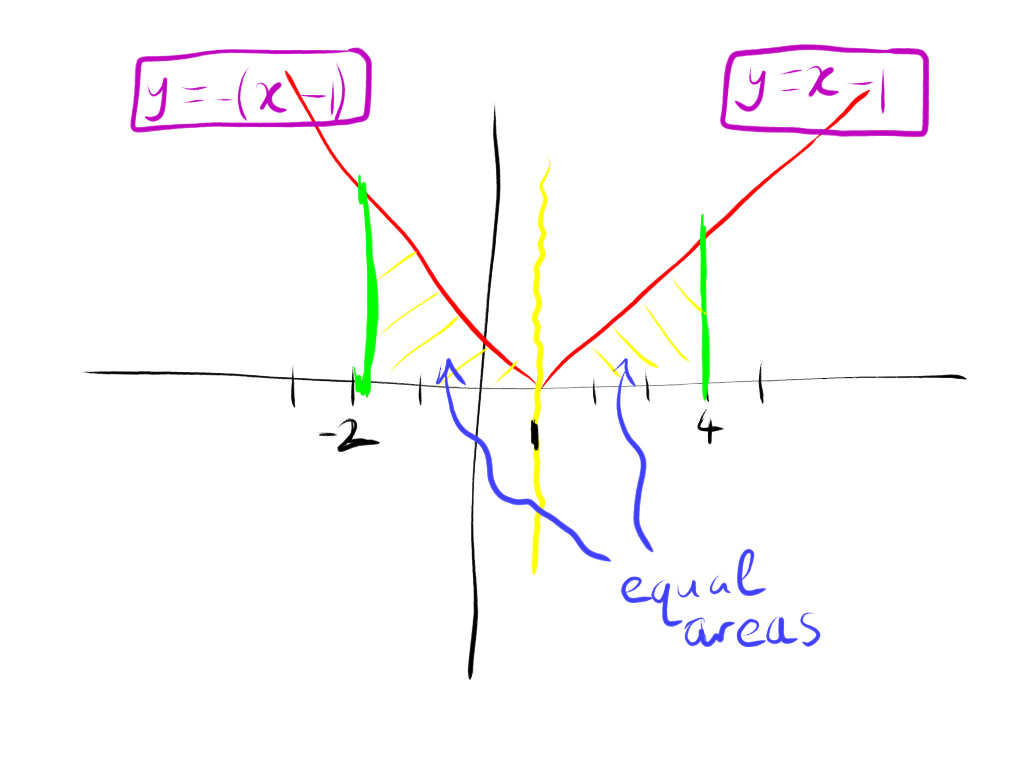
But moving on to the real stuff, we just need to break that absolute vaue thing out
and
so first we split the integral
switching the limits on the second integral
We could also have recognised the symmetry, namely that the
which becomes apparent from sketching the function itself