How do you solve #log_5(x+1) - log_4(x-2) = 1#?
1 Answer
I wanted to provide a graphical approach to this problem...
The answer to this problem is where the function,
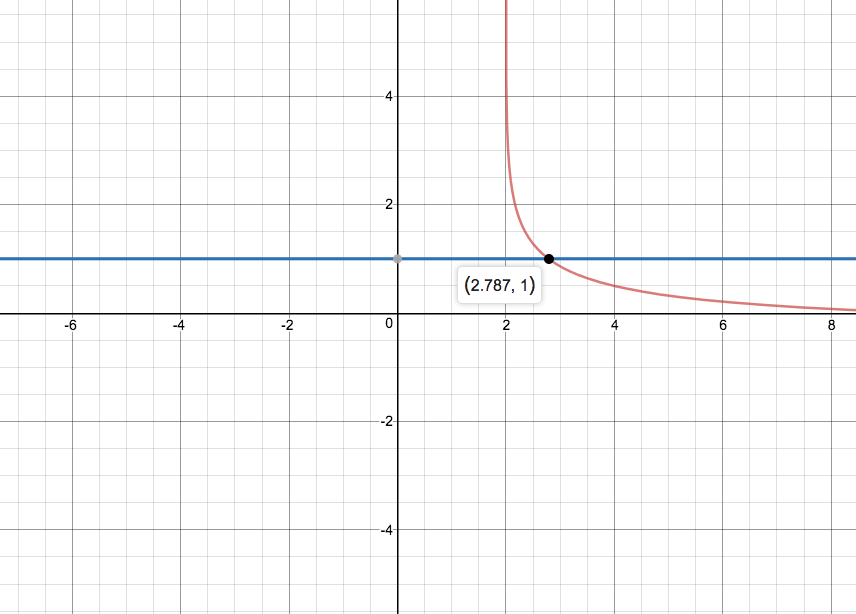
Hence from this graph we see that
Now i understand that this is not the most ellegant solution, and not the traditional method, so i want to hopefully start a more rigerouse approach:
We could possibly use a very forgotten identity in logarithms...
If you have never seen this before, its a good idea to add this to your inventory of identities...
Applying this...
Now maybe we can use binomial epxansion and other approximations, but i hope this was a good start to one apporach, but maybe there are more simple approaches, hopefully someone else can provide such a method!

