How do you solve the following linear system -2x+y=5, 4x-2y=9 ?
1 Answer
Ø (No solutions), they are parallel lines.
Explanation:
There are 3 possible ways of solving systems of equations.
1.) Solving w/ elimination
2.) Solving w/ graphing
3.) Solving w/ substitution
Plotting these two equations on an online graphing calculator called Desmos: 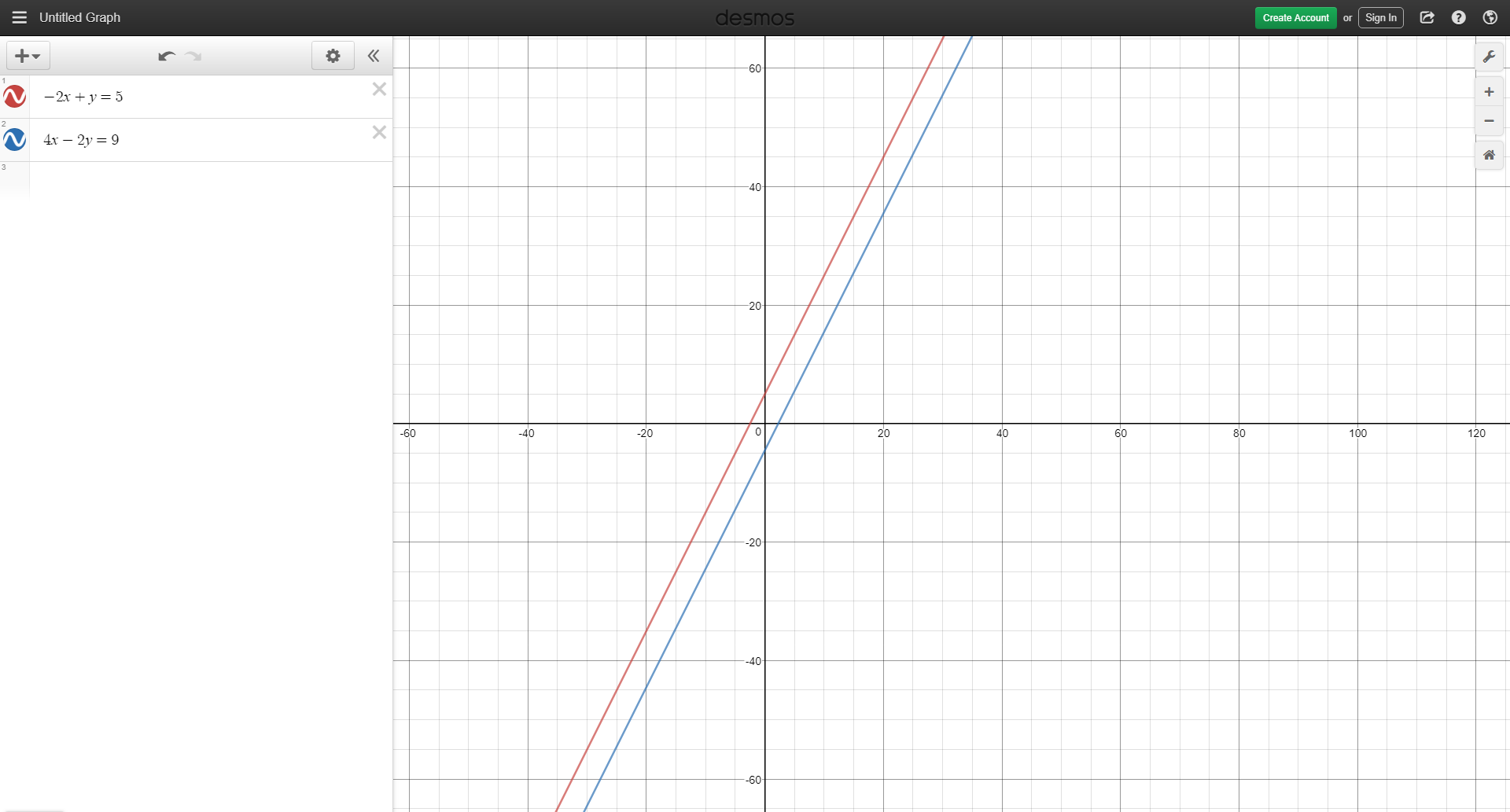
The two lines appear to be parallel...
Let's try to prove it by solving w/ substitution:
We have equation ①
①
①
②
①&② combined:
①&②
①&②
There are three types of possible results for linear equations, infinite solutions, one solution, or no solutions. This is an invalid statement, which means there are no valid solutions, often represented with the character Ø. As a result of this, this means the lines are parallel to each other.
- For more reading on solving systems of equations, check out this resource
- For more reading on solving solutions, check out this resource
Hope this helps!

