How do you solve the following system?

Question

#a_1x_1+a_2x_2+a_3=0#, #a_4x_1+a_5x_2+a_6=0#

1469 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-21T20:43:34

#(x_1,x_2)=((a_2a_6-a_3a_5)/(a_1a_5-a_2a_4) , (a_3a_4-a_1a_6)/(a_1a_5-a_2a_4))#

Here,

#a_1x_1+a_2x_2=-a_3...to(1),where, a_1,a_2,a_3 inRR#

#a_4x_1+a_5x_2=-a_6...to(2) ,where ,a_4,a_5,a_6 in RR#

#"using "color(blue)"Cramer's Rule" # #"to solve the system :"#

First we find determinants : #D ,D_x and D_y#

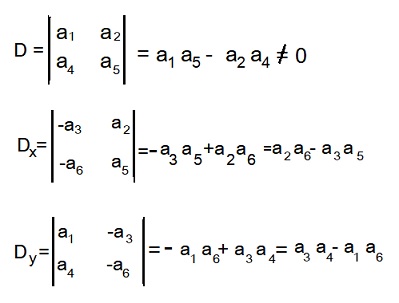
enter image source here
#"Cramer's Rule :"#

#x_1=(D_x)/D =(a_2a_6-a_3a_5)/(a_1a_5-a_2a_4) ,where, a_1a_5-a_2a_4!=0#

#x_2=(D_y)/D =(a_3a_4-a_1a_6)/(a_1a_5-a_2a_4) , where, a_1a_5-a_2a_4!=0#

Hence, the solution of system is :

#(x_1,x_2)=((a_2a_6-a_3a_5)/(a_1a_5-a_2a_4) , (a_3a_4-a_1a_6)/(a_1a_5-a_2a_4)),#

#where, a_1a_5-a_2a_4!=0#