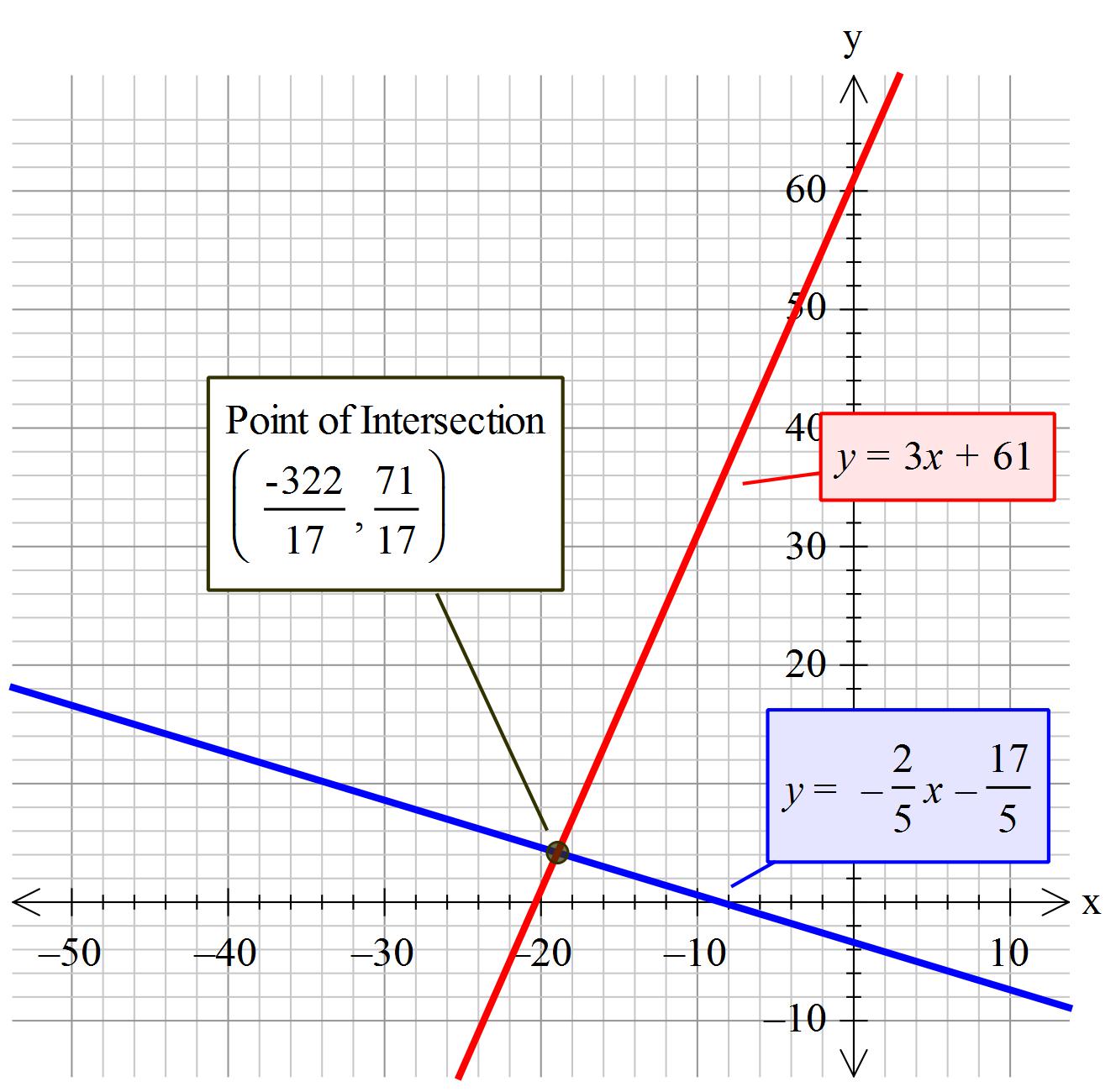
How do you solve the following system?: #-2x -5y =17, 3x -y = -61#
1 Answer
The joint values that satisfy both equations are:
Explanation:
These are equations of straight line graphs. The gradients are different which means that at some point they will cross.
At that instance they will both share the same values for
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Write equation (2) as :
Using
so that we have only 1 unknown variable
Multiply out the brackets
add 305 to both sides
Multiply both sides by (-1)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute for