Question

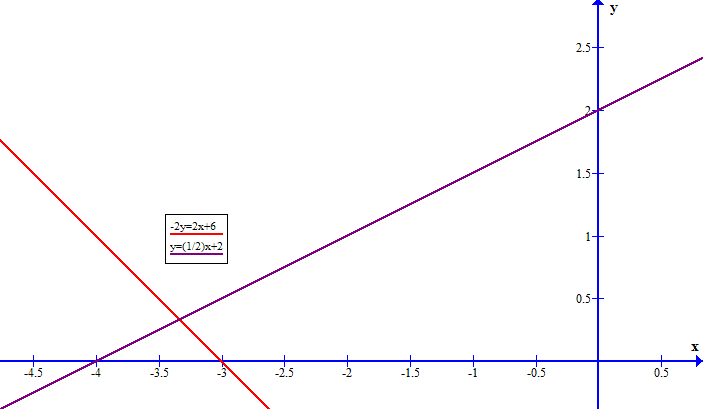
How do you solve the following system?: `-2y=2x+6 , y= 1/2x +2`

Answer 1

`(x,y)=(-3 1/3, 1/3)`

Explanation:

Given
[1]`color(white)("XXX")-2y=2x+6`
[2]`color(white)("XXX")y=1/2x+2`

Multiplying both sides of [2] by `(-2)`
[3]`color(white)("XXX")-2y=-x-4`

Since the left sides of [1] and [3] are equal
the right sides must also be equal
[4]`color(white)("XXX")2x+6=-x-4`

Adding `x` to both sides of [4]
[5]`color(white)("XXX")3x+6=-4`

Subtracting `6` from both sides of [5]
[6]`color(white)("XXX")3x=-10`

Dividing both sides of [6] by `3`
[7]`color(white)("XXX")x=-10/3 (=-3 1/3)`

Substituting `(-10/3)` for `x` in [2]
[8]`color(white)("XXX")y=1/2xx(-10/3)+2`

`color(white)("XXXXX")=-5/3+2`

`color(white)("XXXXX")=1/3`

`(x,y)=(-10/3,1/3)`

The graphic solution (below) supports this result: