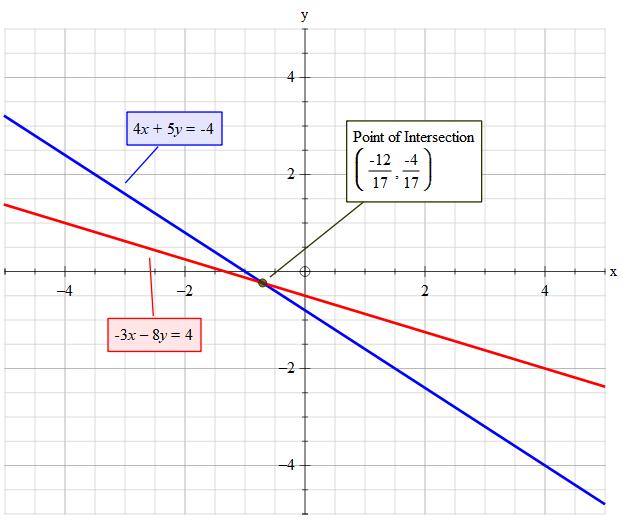
Given:
#4x+5y=-4" "...........................Equation(1)#
#-3x-8y=4" "............................Equation(2)#
2 equations and 2 unknowns. Thus solvable.
We need to end up with one equation and 1 unknown.
#color(blue)("'Getting rid' of the "x" term")#
#[color(white)("d")3xxEqn(1)color(white)(2/2)]+[color(white)("d")4xxEqn(2)color(white)(2/2)]#
#color(white)("d.")12x+15y=-12" "........................Equation(1_a)#
#ul(-12x-32y=color(white)("d..")16)" "........................Equation(2_a)#
#color(white)("dd")0color(white)(".d")-17y=+4#
Divide both sides by #-17#
#color(white)("dddddddd")y=-4/17#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("'Getting rid' of the "y" term")#
Substitute #-4/17# for #y#
I choose #Eqn(1)# as all the left side of = is positive.
It will still work if you choose #Eqn(2)#
#color(green)( 4x+5color(red)(y)=-4 color(white)("dddd")->color(white)("dddd")4x+5(color(red)(-4/17))=-4 )#
#color(white)("dddddddddddddddd")->color(white)("dddd")4xcolor(white)("ddd")-20/17color(white)("dd")=-4#
Add #20/17# to both sides
#color(white)("dddddddddddddddd")->color(white)("dddd")4xcolor(white)("dd")=-4+20/17#
#color(white)("dddddddddddddddd")->color(white)("dddd")4x=-48/17#
Divide both sides by 4
#color(white)("ddddddddddddddd")->color(white)("dddd")x=-12/17#