7n^2 + 6 = -407n2+6=−40
To use the quadratic formula to find the zeroes, we need to make sure the equation is written in the form color(red)(a)x^2 + color(magenta)(b)x + color(blue)(c) = 0ax2+bx+c=0.
To do so, we need to add color(orange)4040 to both sides of the equation:
7n^2 + 6 quadcolor(orange)(+quad40) = -40 quadcolor(orange)(+quad40)
7n^2 + 46 = 0
So we know that:
color(red)(a = 7)
color(magenta)(b = 0)
color(blue)(c = 46)
The quadratic formula is x = (-color(magenta)(b) +- sqrt(color(magenta)(b)^2 - 4color(red)(a)color(blue)(c)))/(2color(red)(a)).
Now we can plug in the values for color(red)(a), color(magenta)(b), and color(blue)(c) into the quadratic formula:
x = (-color(magenta)(0) +- sqrt((color(magenta)(0))^2 - 4(color(red)(7))(color(blue)(46))))/(2(color(red)(7)))
Simplify:
x = (+- sqrt(-1288))/14
The solution is imaginary since we cannot take the square root of a negative number.
However, we know that i, or imaginary, is equal to sqrt(-1). Therefore, we can factor out a -1 from the square root and make it an i:
x = (+-isqrt(1288))/14
x = (+- 2isqrt(322))/14
x = (+- isqrt322)/7
This is the same thing as:
x = (isqrt322)/7 and x = (-isqrt322)/7
because +- means "plus or minus."
To clarify, this doesn't mean that there is a zero or root. This is an imaginary solution, meaning that there are no zeros. To prove this, let's look at the graph of this equation:
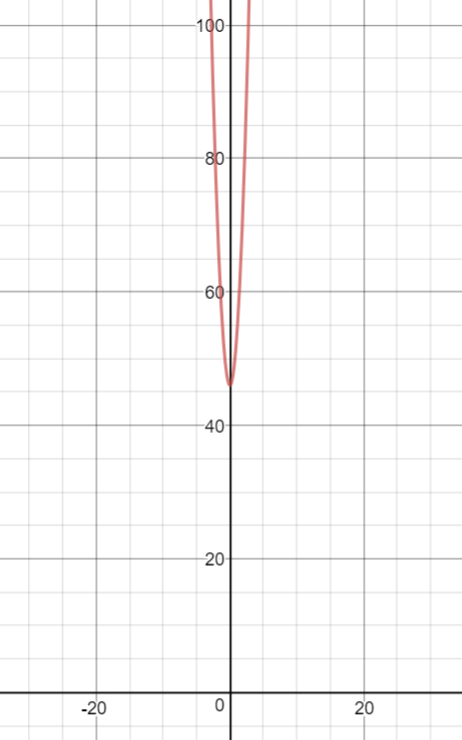
(desmos.com)
As you can see, there are no zeroes. The vertex starts above the x-axis.
Hope this helps!


