Question

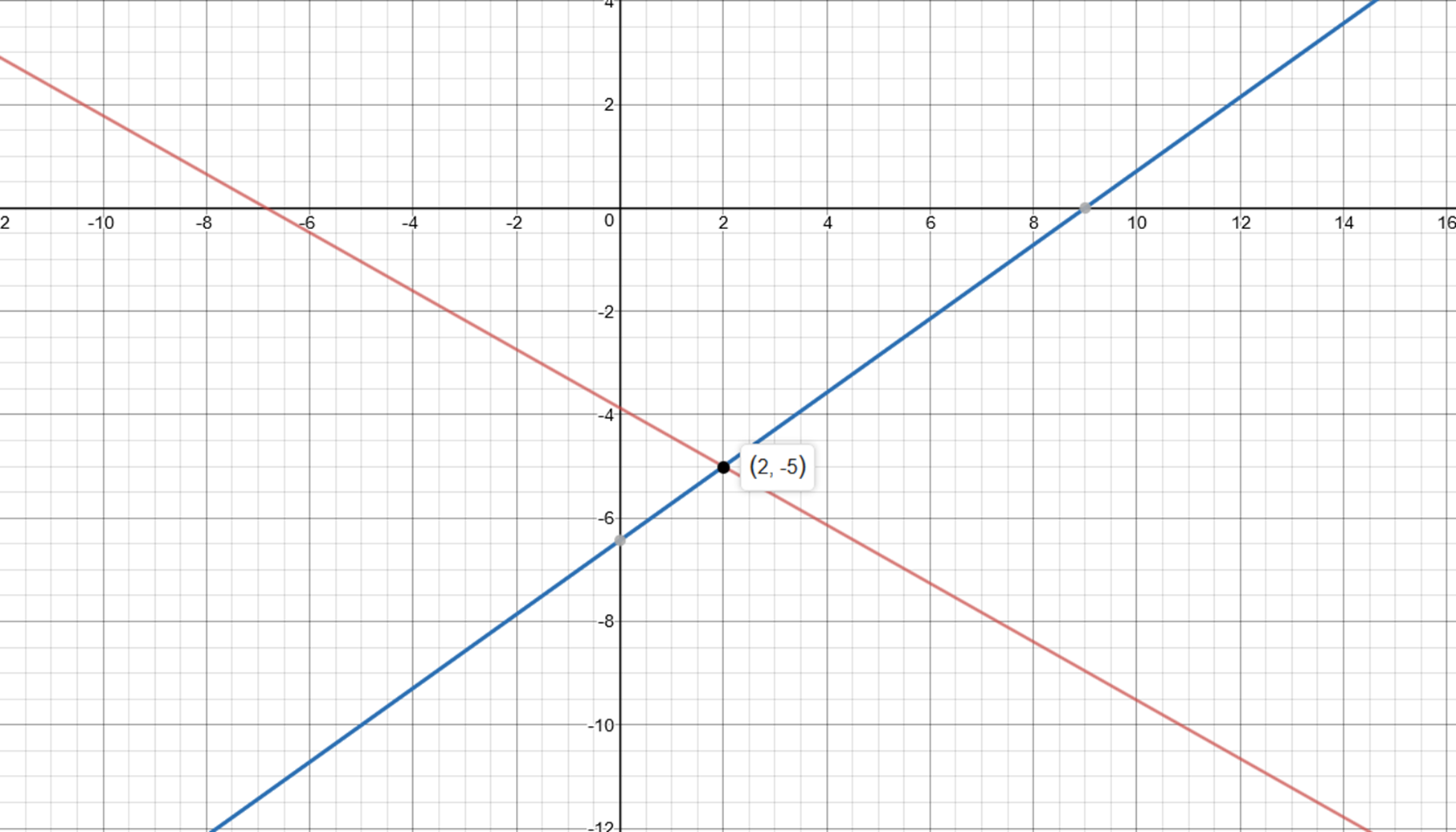
How do you solve the system of equations `13x + 23y = - 89` and `10x - 14y =90`?

Answer 1

`color(green)(x = 2, y = -5`

Explanation:

`13x + 23y = -89, " Eqn (1)"`

`10x - 14y = 90, " Eqn (2)"`

`130 x + 230 y = - 890, " Multiply Eqn (1) by 10", color(red)(" Eqn (3)"`

`130 x - 182 y = 1170, " Multiply Eqn (2) by 13", color(red)(" Eqn (4)"`

`cancel(130x) + 230 y - cancel(130x) + 182 y = -890 - 1170, color(red)(" subtracting Eqn (4) from Eqn (3)"`

`412 y = -2060,color(blue)( y = -5`

Substituting value of y in Eqn (1),

`13x + (23 * -5) = -89`

`13 x = - 89 + 115`

`color(blue)(x = 26 / 13 = 2`

Answer 2

`x=2`
`y=-5`

Explanation:

Given -

`13x+23y=-89` ----------(1) `xx 10`
`10x-14y=90` ----------(2) `xx 13`

`130x +230y=-890` ------- (3)
`130x-182y=1170` -------(4) ----`(3)-(4)`

`412y=-2060`

`y=(-2060)/(412)=-5`

`y=-5`

Substitute `y=-5` in equation (1)

`13x+23(-5)=-89`

`13x-115=-89`

`13x=-89+115=26`

`x=26/13=2`

`x=2`