Question

How do you solve this compound inequality `2x + 6\geq 12 or 2x + 6\leq - 4`?

Answer 1

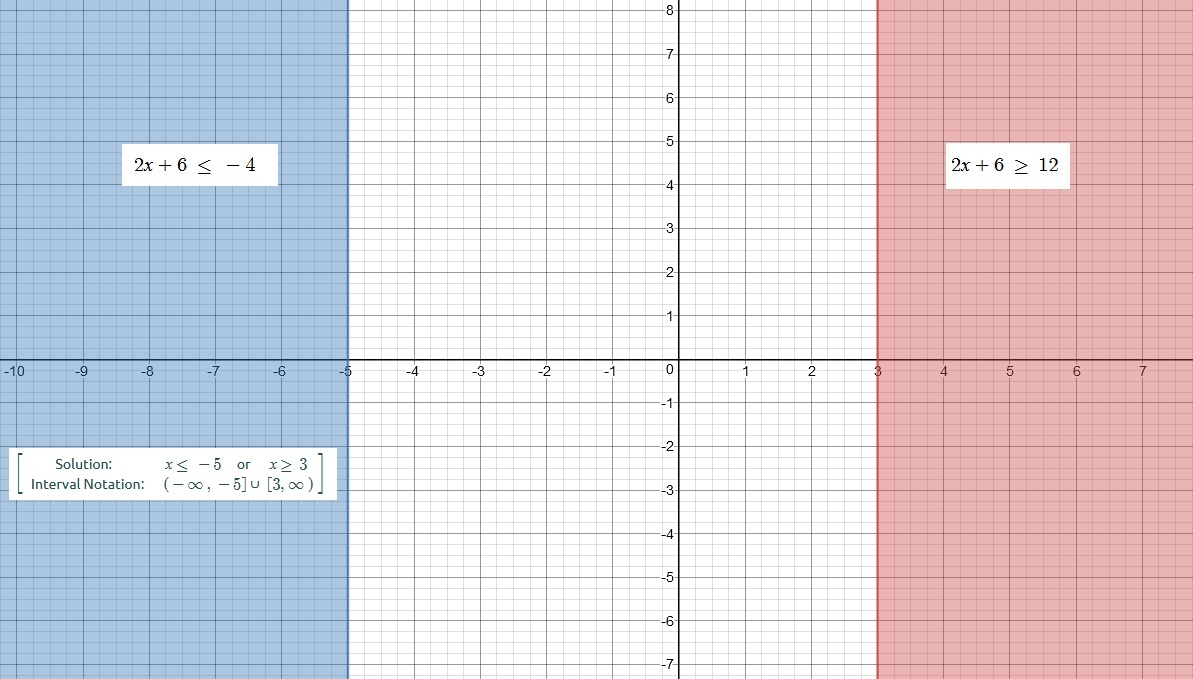
Our solution:

`color(red)( x <= -5 or x >= 3)`

Using Interval Notation:

`color(blue)((-oo, -5] uu [3, oo)`

Graph available supporting our solution.

Explanation:

We have a Compound Inequality :-

`color(green)(2x + 6 >= 12 or 2x + 6 <= -4)`

We will consider our compound inequality as two individual parts to start with:

`color(green)(2x + 6 >= 12` . . . Inequality.1

`color(green)(2x + 6 <= -4)` . . . Inequality.2

We will start with . . . Inequality.2 first:

`color(green)(2x + 6 <= -4)` . . .Inequality.2

Add `-6` to both sides of our inequality:

`color(green)(2x + cancel (+6) cancel(- 6) <= -4 - 6`

`color(green)(rArr 2x <= -10`

Divide both sides of the inequality by `2`

`color(green)(rArr (cancel 2x)/cancel 2 >= -10/2`

`color(green)(rArr x >= -5` `color(red)( ... Intermediate.Answer.1)`

Next we will consider . . . Inequality.1 :

`color(green)(2x + 6 >= 12` . . . Inequality.1

Add `-6` to both sides of our inequality:

`color(green)(2x + cancel (+6) cancel(- 6) >= 12 - 6`

`color(green)(rArr 2x >= 6`

Divide both sides of the inequality by `2`

`color(green)(rArr (cancel 2x)/cancel 2 >= 6/2`

`color(green)(rArr x >= 3` `color(red)( ... Intermediate.Answer.2)`

Using our intermediate answers 1 and 2 we can write our solutions as:

`color(red)( x <= -5 or x >= 3)`

Using Interval Notation:

`color(blue)((-oo, -5] uu [3, oo)`

Refer to the graph below for a better understanding:

I hope you find this solution useful.