Question

How do you solve this system of inequalities: `y < \frac { 1} { 3} x + 4 and y \geq - x + 1`?

Answer 1

`color(blue)((1/3)x+4 > y >= -x+1`

Explanation:

Given:

We are given the System of Inequalities:

`color(brown)(y < (1/3)x+4` and

`color(brown)(y >= (-x)+1`

`color(green)(Step.1`

`color(brown)(y < (1/3)x+4` - Image of the graph created using GeoGebra

`color(green)(Step.2`

`color(brown)(y >= (-x)+1` - Image of the graph created using GeoGebra

`color(green)(Step.3`

`color(brown)(y < (1/3)x+4` and `color(brown)(y >= (-x)+1` - Image of the combined graphs created using GeoGebra

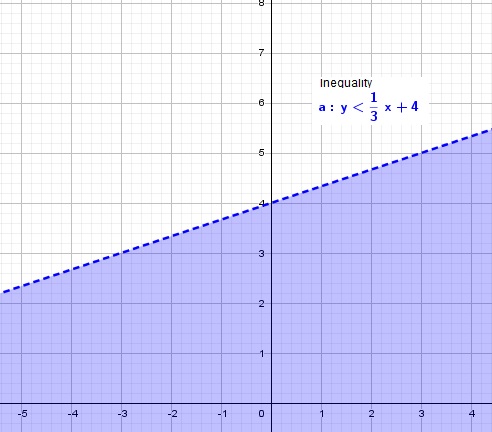
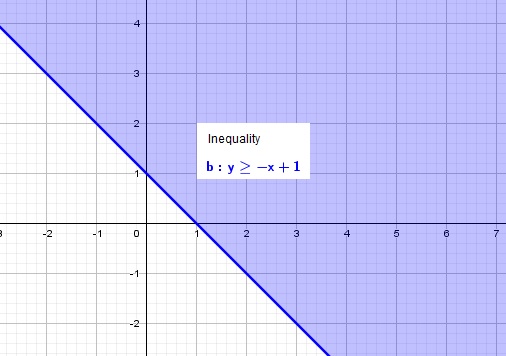
If you observe closely, you will find the solution in a visual form.

The solution to the system of inequalities is the darker shaded region, which is the overlap of the two individual regions.

`color(green)(Step.4`

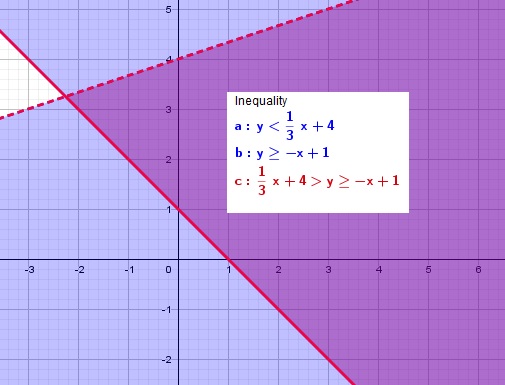
If you want to view just the solutions, please refer to the image below:

Note:

If the inequality is < or >, graph of the equation has a dotted line.

If the inequality is ≤ or ≥, graph of the equation has a solid line.

This line divides the xy- plane into two regions: a region that satisfies the inequality, and a region that does not.