Question

How do you solve `x^ { 2} - 12= - 3`?

Answer 1

`x=+-3`

Explanation:

`"isolate "x^2" by adding 12 to each side of the equation"`

`x^2=-3+12=9`

`color(blue)"take the square root of both sides"`

`sqrt(x^2)=+-sqrt9larrcolor(blue)"note plus or minus"`

`x=+-3`

Answer 2

`x=+-3`

Explanation:

First thing that you should do if you want to solve it mathematically is to pass the terms with are on the right of the equation to the right or viceversa. You then have:

`x^2-9=0`

Then you make use of the quadratic equations formula: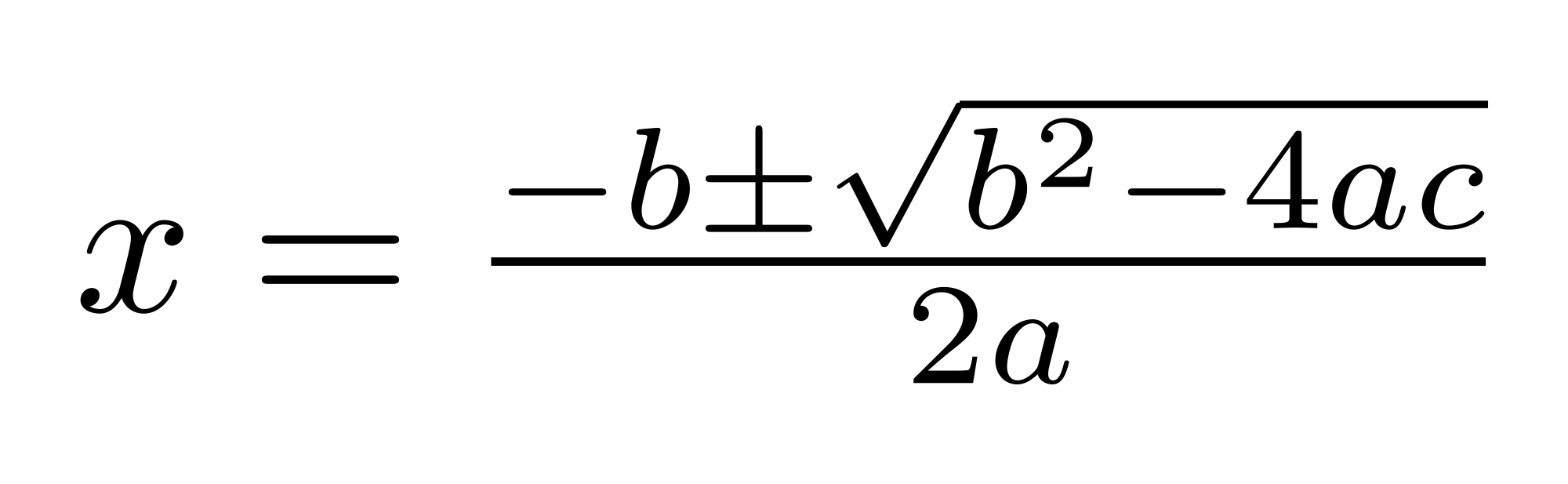

, where a, b and c are the 2nd order, 1st order and independent terms in the equation. This is, in your case, `a=1`, because 1 x X^2, `b=0`, because 0 x X, and `c=-9`. If you substitute, you will get `x=+-3` as solution.

Hint: For simple equations like this one, think first about simple quadratic rules. `x^2=9` can be directly solved if you think that `+-3^2` is equal to `9`.