How do you solve #x^ { 2} - 16x + 60> 0#?
1 Answer
Mar 14, 2017
Explanation:
The first step is to factorise the quadratic.
#rArr(x-6)(x-10)>0# The quadratic will therefore be zero at x = 6 and x = 10
These values are useful in that these are the values where the function crosses the x- axis. That is changes from positive to negative or negative to positive.
These zeroes divide the x-axis into 3 intervals and by considering each interval , using a
#color(blue)"factor table"# we can determine where the function is greater/less than zero.The 3 intervals are
#(-oo,6),(6,10),(10,+oo)#
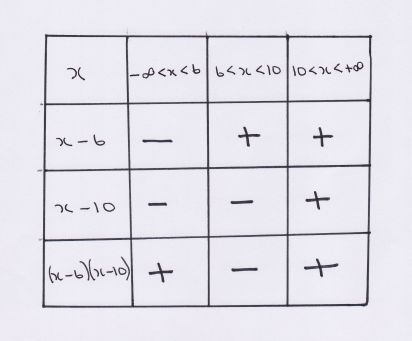
We require the intervals that are positive for the solution.
#rArrx^2-16x+60>0#
#rArr(-oo,6)uu(10,+oo)#
graph{x^2-16x+60 [-11.1, 11.1, -5.55, 5.55]}
