Question

How do you solve `(x ^ { 5} - 15x ^ { 4} + 90x ^ { 3} - 270x^ { 2} + 405x - 243) -: ( x - 3)`?

Answer 1

`(x^5-15x^4+90x^3-270x^2+405x-243)/(x-3) = x^4-12x^3+54x^2-108x+81`

Explanation:

What follows is not the quickest way, but it does exercise the binomial theorem a bit...

The quintic looks a suspiciously like `(x-3)^5`. Let's check...

By the binomial theorem:

`(a+b)^5 = sum_(k=0)^5 ((5),(k)) a^(5-k) b^k`

where `((5),(k)) = (5!)/((5-k)! k!)`

These binomial coefficients can be read from the sixth row of Pascal's triangle...

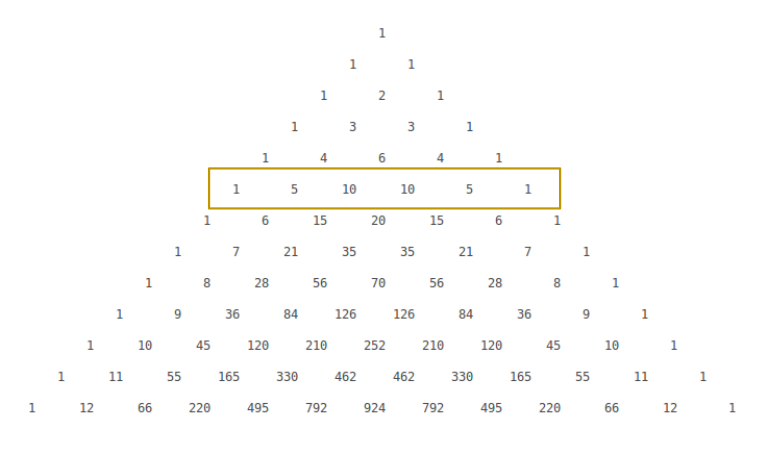
So we find:

`(a+b)^5 = a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5`

Putting `a=x` and `b=-3` we get:

`(x-3)^5 = x^5+5(-3)x^4+10(-3)^2x^3+10(-3)^3x^2+5(-3)^4x+(-3)^5`

`color(white)((x-3)^5) = x^5-15x^4+90x^3-270x^2+405x-243`

Similarly, using the fifth row of Pascal's triangle, we have:

`(x-3)^4 = x^4+4(-3)x^3+6(-3)^2x^2+4(-3)^3x+(-3)^4`

`color(white)((x-3)^4) = x^4-12x^3+54x^2-108x+81`

Hence:

`(x^5-15x^4+90x^3-270x^2+405x-243)/(x-3)`

`= (x-3)^5/(x-3)`

`= (x-3)^4`

`= x^4-12x^3+54x^2-108x+81`

Answer 2

`(x^5-15x^4+90x^3-270x^2+405x-243)/(x-3)`

`= x^4-12x^3+54x^2-108x+81`

Explanation:

Here's how I would do it myself.

Write the beginning of the factorisation:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(`

Then examine each power of `x` in turn in descending order to work out what the next term needs to be.

The first term we need to add is `x^4` in order to get `x^5` when multiplied:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(color(blue)(x^4)`

Examining what we have so far, the `(-3)*x^4` will result in `-3x^4`, when what we want for the next product is `-15x^4`. So we want an extra `-12x^4`. We can get this by writing `-12x^3` as our next term:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(x^4color(blue)(-12x^3)`

Then `(-3)(-12x^3) = 36x^3`, but we want `90x^3`, so we need an extra `54x^3`. We can get this by making our next term `54x^2`:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(x^4-12x^3+color(blue)(54x^2)`

Then `(-3)(54x^2) = -162x^2`, but we want `-270x^2`, so we need an extra `-108x^2`. We can get this by making our next term `-108x`:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(x^4-12x^3+54x^2color(blue)(-108x)`

Then `(-3)(-108x) = 324x`, but we want `405x`, so we need an extra `81x`. We can get this by making our next term `81`:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(x^4-12x^3+54x^2-108x+color(blue)(81))`

Finally, note that `(-3)(81) = -243`, just as we want. So the factorisation is exact.

I have used quite a few words to describe it, but most of the calculations can be done in your head without having to write down more than:

`(x^5-15x^4+90x^3-270x^2+405x-243) = (x-3)(x^4-12x^3+54x^2-108x+81)`

Hence:

`(x^5-15x^4+90x^3-270x^2+405x-243)/(x-3)`

`= x^4-12x^3+54x^2-108x+81`