How do you solve $(x + 7) (2 x + 5) = - 7$ $(x + 7) ( 2x + 5) = - 7$ ?

Question

How do you solve $(x + 7) (2 x + 5) = - 7$ $(x + 7) ( 2x + 5) = - 7$ ?

2 Answers

Impact of this question

1626 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-26T02:17:31

$x = - 6, - \frac{7}{2}$ $x=-6,-7/2$

Explanation:

Solve:

$(x + 7) (2 x + 5) = - 7$ $(x+7)(2x+5)=-7$

Expand the left side using the FOIL method.
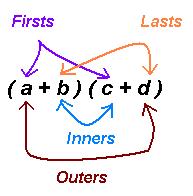
![http://www.mathcaptain.com/algebra/http://foil-method.html](https://useruploads.socratic.org/EkVVTu85STaAPo2aPAV6_foil-method.JPG)

$2 x^{2} + 19 x + 35 = - 7$ $2x^2+19x+35=-7$

Add $7$ $7$ to both sides.

$2 x^{2} + 19 x + 35 + 7 = 0$ $2x^2+19x+35+7=0$

Simplify.

$2 x^{2} + 19 x + 42 = 0$ $2x^2+19x+42=0$

Factor the left-hand side.

$(x + 6) (2 x + 7) = 0$ $(x+6)(2x+7)=0$

Set each binomial equal to zero and solve.

$(x + 6) = 0$ $(x+6)=0$

$x = - 6$ $x=-6$

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

$(2 x + 7) = 0$ $(2x+7)=0$

$2 x = - 7$ $2x=-7$

Divide both sides by $2$ $2$ .

$x = - \frac{7}{2}$ $x=-7/2$

Answer 2 · 2017-07-26T02:21:20

$x = - \frac{7}{2} = - 3 \frac{1}{2}$ $x=-7/2=-3 1/2$ or $x = - 6$ $x=-6$

Explanation:

$(x + 7) (2 x + 5) = - 7$ $(x+7)(2x+5)=-7$

Expand the brackets.

$x (2 x + 5) + 7 (2 x + 5) = - 7$ $x(2x+5)+7(2x+5)=-7$

$2 x^{2} + 5 x + 14 x + 35 = - 7$ $2x^2+5x+14x+35=-7$

$2 x^{2} + 19 x + 35 = - 7$ $2x^2+19x+35=-7$

Add $7$ $7$ to both sides.

$2 x^{2} + 19 x + 35 + 7 = 7 - 7$ $2x^2+19x+35+7=7-7$

$2 x^{2} + 19 x + 42 = 0$ $2x^2+19x+42=0$

Factorise.

$2 x^{2} + 12 x + 7 x + 42 = 0$ $2x^2+12x+7x+42=0$

$2 x (x + 6) + 7 (x + 6) = 0$ $2x(x+6)+7(x+6)=0$

$(2 x + 7) (x + 6) = 0$ $(2x+7)(x+6)=0$

$2 x + 7 = 0$ $2x+7=0$ and $x + 6 = 0$ $x+6=0$

$x = - \frac{7}{2}$ $x=-7/2$ or $x = - 6$ $x=-6$

Science

Math

Humanities

... and beyond

How do you solve $(x + 7) (2 x + 5) = - 7$ $(x + 7) ( 2x + 5) = - 7$ ?

2 Answers

Explanation:

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you solve (x+7)(2x+5)=−7(x + 7) ( 2x + 5) = - 7?

2 Answers

Explanation:

Explanation:

Related questions

Impact of this question

How do you solve $(x + 7) (2 x + 5) = - 7$ $(x + 7) ( 2x + 5) = - 7$ ?