How do you solve #y^{ 2} - 15y + 54\geq 0#?

1 Answer
Sridhar V.
Dec 2, 2017

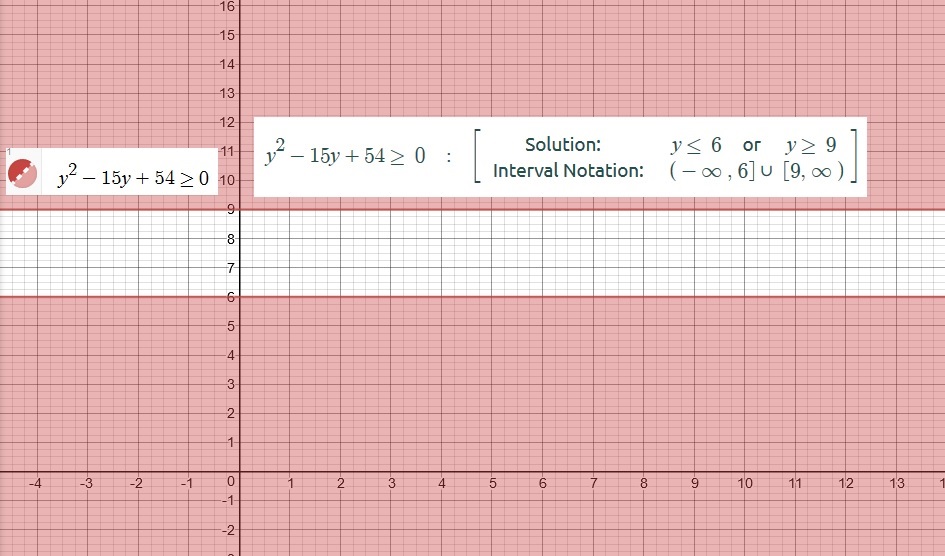
Solutions:
#y <= 6 or y >=9#

Using Interval Notations :
#(-oo, 6] uu [9, oo)#

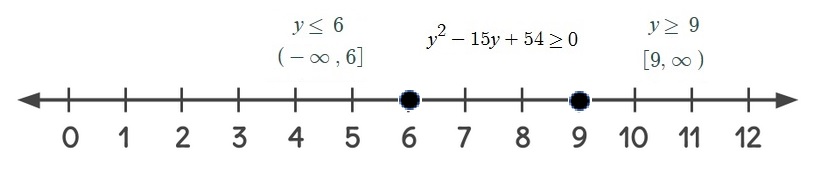
enter image source here

Explanation:

Graph attached as visual proof of our required solutions.

We have the following Quadratic Inequality given to us:

#y^2 - 15y + 54 >= 0#

We can factorize the quadratic expression on the left-hand side as follows and rewrite our quadratic inequality :

#y^2 - 9y - 6y + 54 >= 0#

#rArr y(y -9) -6(y - 9) >= 0#

Therefore, #(y -9)(y - 6) >= 0#

Hence, #(y - 9) =0 or (y -6 ) =0#

We get two values for #y#.

They are #y =9, y = 6#

Next step is to choose values for #y# as follows, to test them on the Number Line:

A value less than 6; a value #>6# but #<9# and a value #>9# to verify whether our inequality #y^2 - 15y + 54 >= 0# works for these values.

Let these values by #y =5#;#" "y =7# and #y = 10#

When #color(red)(y = 5)#

#5^2 - 15(5) + 54 >= 0#

# 25 - 75 + 54 >=0#

#rArr4 >=0#

We observe that the value #" "y=5# satisfies our inequality

When #color(red)(y = 7)#

#7^2 - 15(7) + 54 >= 0#

# 49 - 105 + 54 >=0#

#rArr-2 >=0#

We observe that the value #" "y=7# does not satisfy our inequality. Hence we must keep this fact in our mind when we indicate our intervals for the inequality.

When #color(red)(y = 10)#

#10^2 - 15(10) + 54 >= 0#

# 100 - 150 + 54 >=0#

#rArr4 >=0#

We observe that the value #" "y=10# satisfies our inequality.

Hence, our solutions to the inequality #y^2 - 15y + 54 >= 0# are given by:

#color(blue)(y <= 6 or y >=9)#

Using Interval Notations our solution set is :

#color(green)((-oo, 6] uu [9, oo))#

Next, we use a Number Line and mark these values of #y#

Please refer to the Image attached for the Number Line.

The graph below will provide a visual evidence of our findings:

enter image source here

Related questions
Impact of this question
1388 views around the world
You can reuse this answer
Creative Commons License