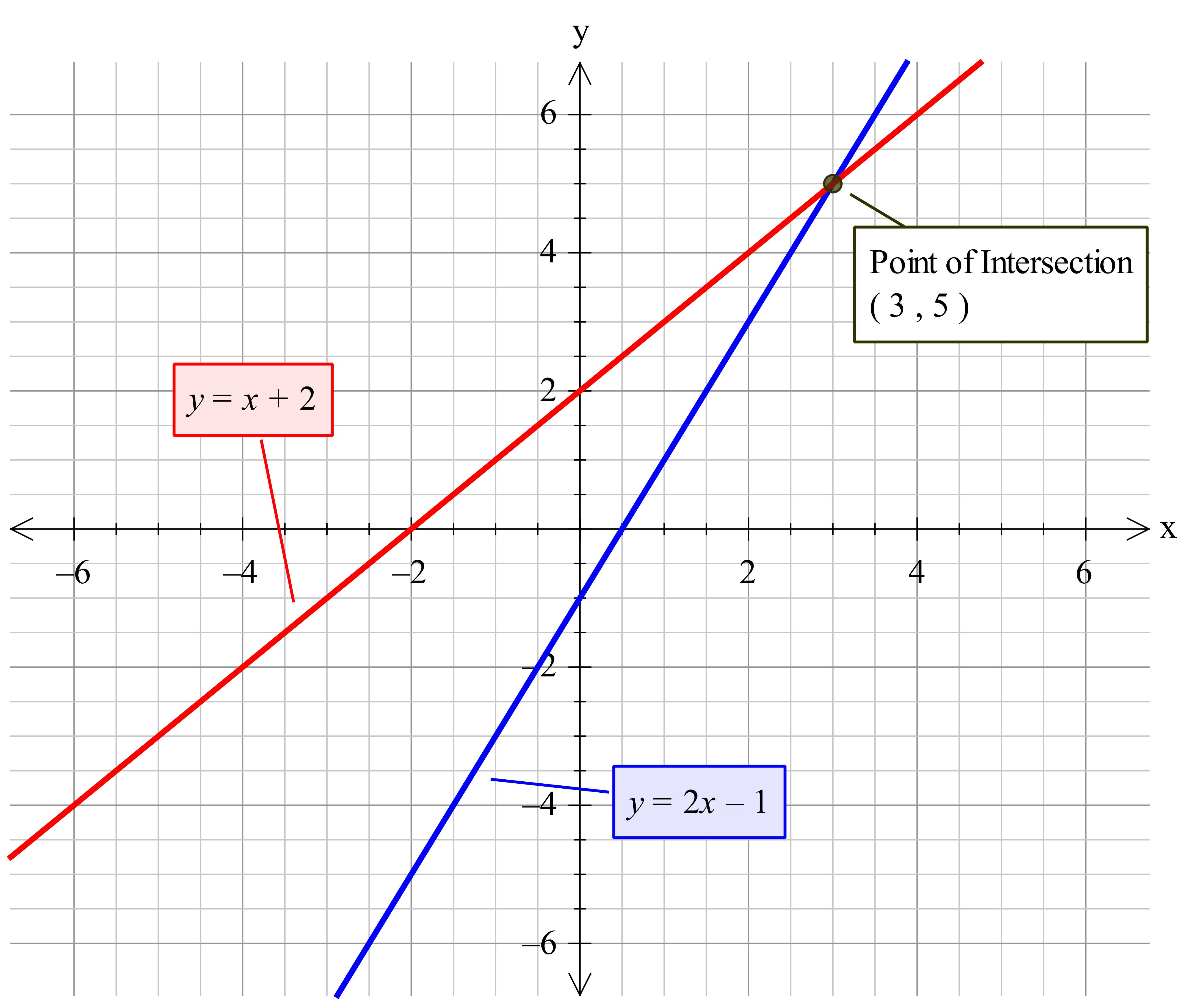
How do you solve y=2x-1 and y=x+2?

Question

15883 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-05T08:57:37

First part of the calculation given in detail so that you can see the method more clearly. The second part uses shortcuts.

Point of intersection #P_1->(x,y)=(3,5)#

Given:

#y=2x-1#....................Equation(1)
#y=x+2#.....................Equation(2)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider equation 2

Subtract #color(blue)(2)# from both sides

#color(brown)(ycolor(blue)(-2)=x+2color(blue)(-2))#

#y-2=x#..........................Equation(3)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using equation(3) substitute for #x# in equation(1)

#y=2(y-2)-1#

#y=2y-4-1#

#y=2y-5#

Subtract #color(blue)(y)# form both sides

#color(brown)(ycolor(blue)(-y)=2ycolor(blue)(-y)-5)#

#0=y-5#

Add 5 to both sides

#y=5#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Substitute #y=5# into either equation(1) or (2). I chose (2)

#y=x+2" "->" "5=x+2#

#x=3#

Tony B