Question

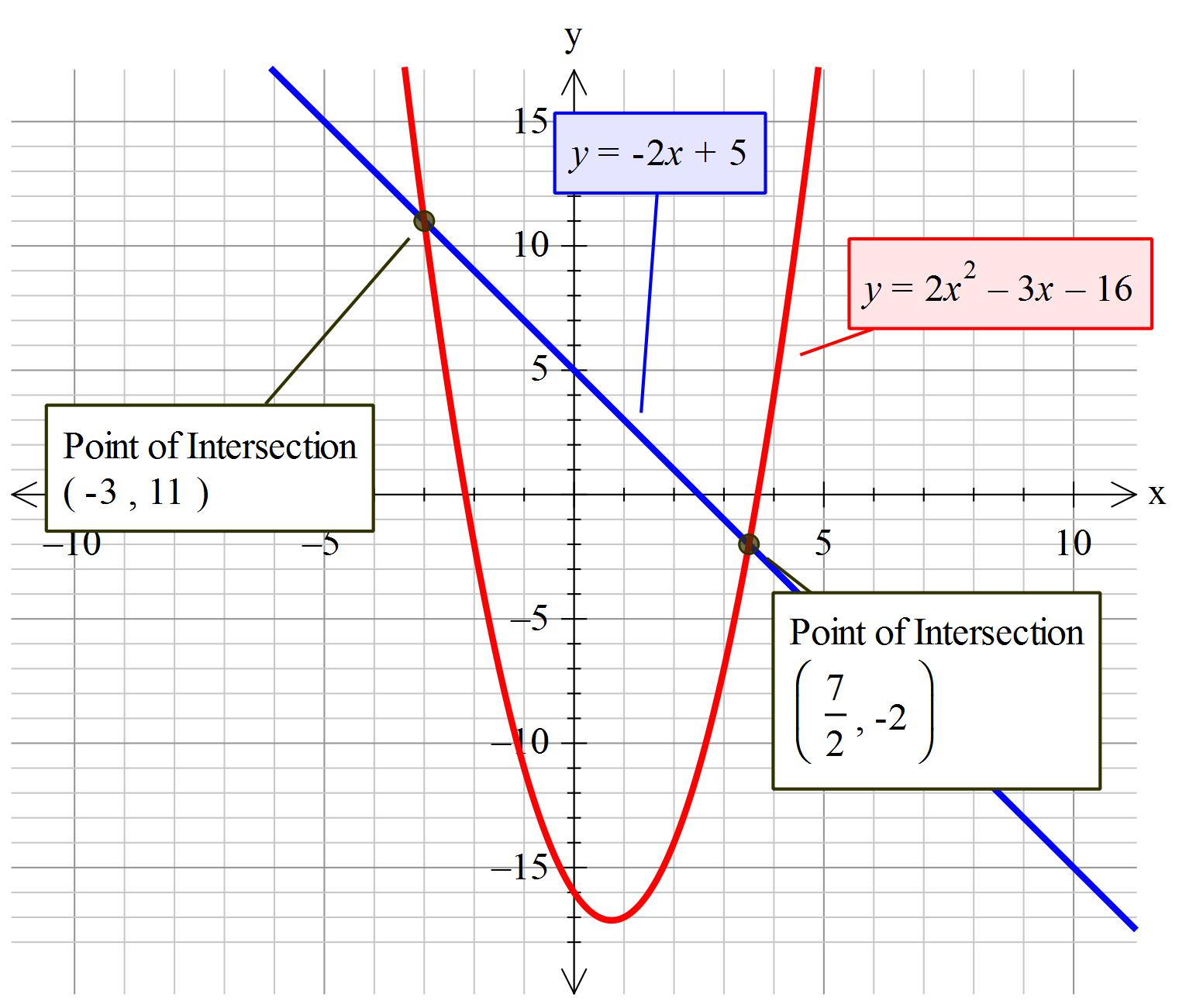
How do you solve `y+2x=5` and `2x^2 - 3x - y =16`?

Answer 1

`A(-3.11)`

`B(7/2,-2)`

Explanation:

In this way:

`y+2x=5`
`2x^2 - 3x - y =16`,

so:

`y=5-2x`

`2x^2-3x-(5-2x)=16rArr2x^2-x-21=0`,

`Delta=b^2-4ac=1-4(2)(-21)=1+168=169=13^2rArr`

`x_(1,2)=(-b+-sqrtDelta)/(2a)=(-(-1)+-13)/(2*2)=(1+-13)/4rArr`

`x_1=(1-13)/4=-12/4=-3` and `y_1=5-2*(-3)=11`
`x_2=(1+13)/4=14/4=7/2` and `y_2=5-2*7/2=-2`.

So:

`A(-3.11)`

`B(7/2,-2)`

Answer 2

`x=7/2" or "x=-3`

Explanation:

Given:
`y+2x=5`........................(1)
`2x^2-3x-y=16`...........(2)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Write equation (1) as:`" "y=-2x+5" "..............(1_a)`
Write equation (2) as:`" "y=2x^2-3x-16" ".......(2_a)`

Equate equation `(1_a)" to "(2_a)` through y

`=>" "-2x+5" "=" "y" "=" "2x^2-3x-16`

Collecting like terms and equation to 0

`" "2x^2-x-21=0`

Solving by quadratic formula method

Standard form`" "-> ax^2+bx+c=0`

Where:`" "x= (-b+-sqrt(b^2-4ac))/(2a)`

`a=2`
`b=-1`
`c=-21`

Thus we have:

`" "x=(+1+-sqrt((-1)^2-4(2)(-21)))/(2(2))`

`=>x=(1+-sqrt(169))/4`

`=>x=(1+-13)/4`

`color(blue)(=>x= 14/4 =7/2 " or "x=-12/4 = -3)`