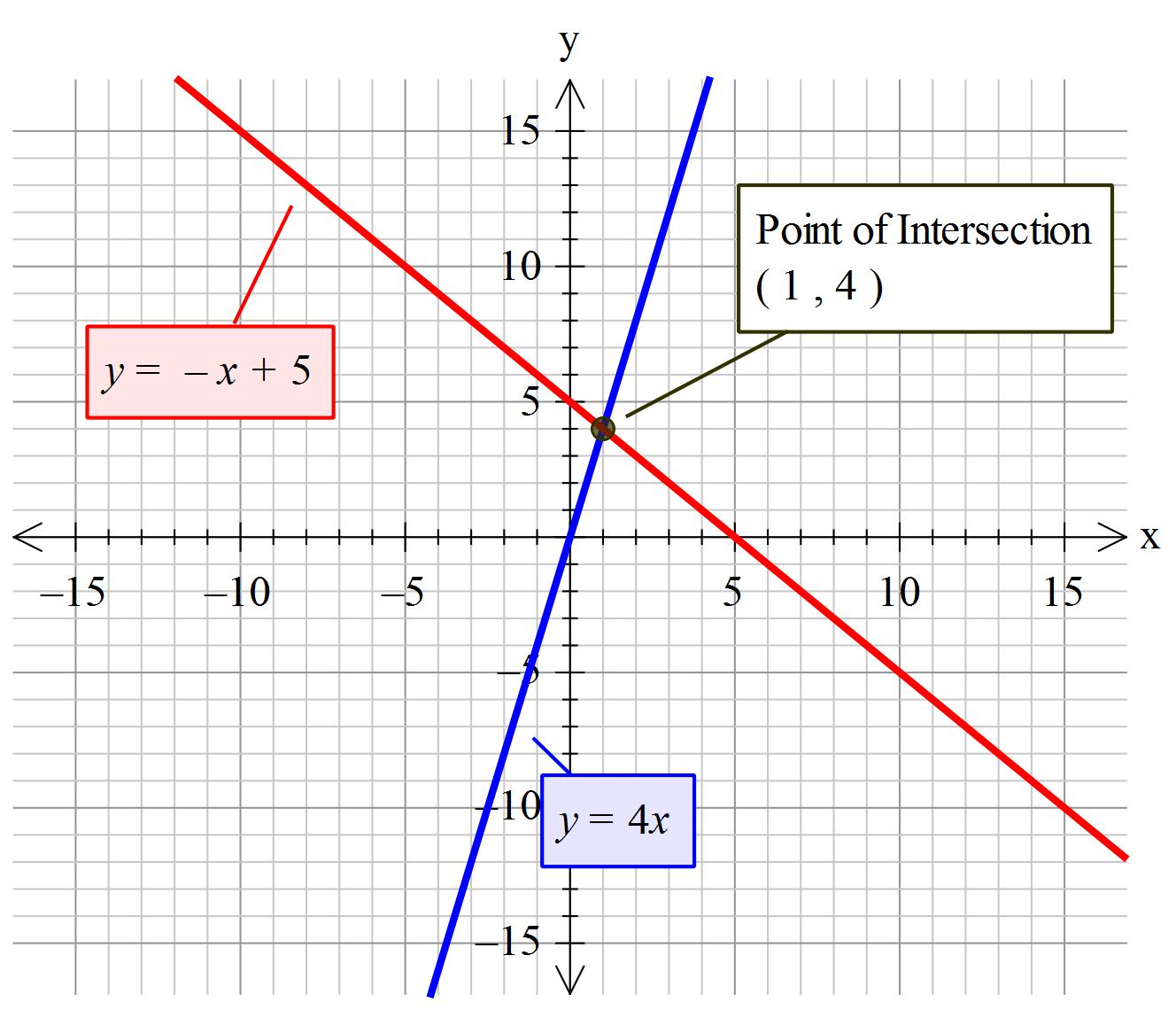
How do you solve #y=4x# and #x+y=5#?
1 Answer
The common point for these two equations ( where the graphs cross) is:
Explanation:
Given:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
To solve for a variable your equation has to end up with just 1 of that variable and no others. That variable has to be on one side of the equals sign and everything else on the others side.
If we substitute for y in equation (2) using what y is worth from equation (1) we have just 1 variable. Which is
But
Divide both sides by 5
But
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute for
In algebra
But
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Note that