Question

How do you use a graph to show that the limit does not exist?

Answer 1

Remember that limits represent the tendency of a function, so limits do not exist if we cannot determine the tendency of the function to a single point. Graphically, limits do not exist when:

1. there is a jump discontinuity
   (Left-Hand Limit `ne` Right-Hand Limit)
   The limit does not exist at `x=1` in the graph below.

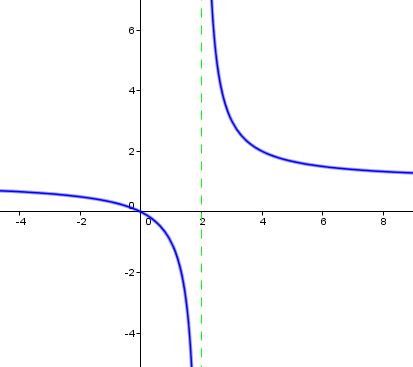
1. there is a vertical asymptote
   (Infinit Limit)
   (Caution: When you have infinite limits, limits do not exist.)
   The limit at `x=2` does not exist in the graph below.

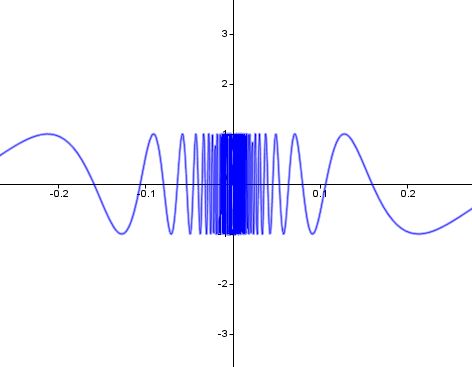
1. there is a violent oscillation
   (e.g., `sin(1/x)` at `x=0`, shown below)

I hope that this was helpful.