How do you use a sum to product formula to find the solution to: sin5x-sinx ?

Question

4890 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-11T11:42:01

# 16 sin^5 x - 20 sin^3 x + 4 sin x #

I'm not sure what a solution means here; we'll write it in terms of cosine and sine of #x.#

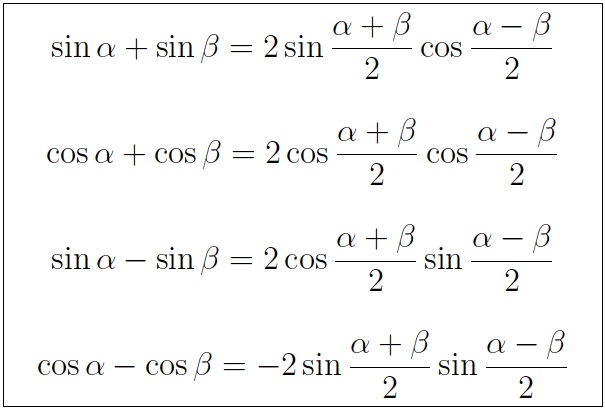
Here's a table of sum/difference to product formulas from Prof. Dave Joyce. We choose the third one, difference of sines:

# sin a - sin b = 2 cos ((a+b)/2) sin ((a-b)/2)#

#sin 5x - sin x= 2 cos(3x) sin(2x) #

#= 2 (4cos^3 x - 3 cos x) (2 sin x cos x) #

#= 4 sin x cos^2 x(4cos ^2 x - 3) #

We have squared cosines so we can turn this into all sines.

#= 4 sin x (1- sin ^2 x)(4 (1- sin ^2 x) - 3) #

#= 4 sin x (1- sin ^2 x)(1- 4sin ^2 x) #

#= 4 sin x (1- 5 sin ^2 x + 4sin ^4 x) #

# sin (5x) - sin x =16 sin^5 x - 20 sin^3 x + 4 sin x #