Question

How do you use double-angle identities to find the exact value of sin 2x & cos 2x when csc(x) = -25/7 and cos x>0?

Answer 1

Find `sinx` first and then find `sin2x` and `cos2x`.

Explanation:

As `cos x` > 0, the basic angle must be in quadrant II or III.
As `csc x` = `-25/7`, the basic angle must be in quadrant III as `csc x` = `1/sin x`.

By algebra, `sin x` = `-7/25`. From there, you can draw the triangle and find out what the basic angle is.

`sin 2x` = `2sin x cos x`
`cos 2x` = `1- 2sin^2x` (there are other variations but this works better for this question)

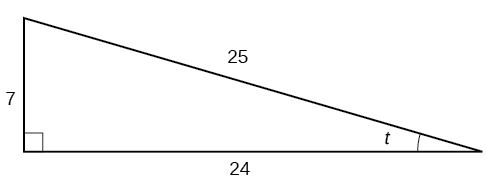
From the triangle, we can find that `cos x = -24/25`
The negative sign is because the basic angle is in the third quadrant, where only tangent is positive,

Evaluating `sin 2x` and `cos 2x`, `sin2x` = `-336/625` and `cos2x` = `-527/625`.

The negative signs are because the angles fall in the third quadrant. Not so sure about that though.