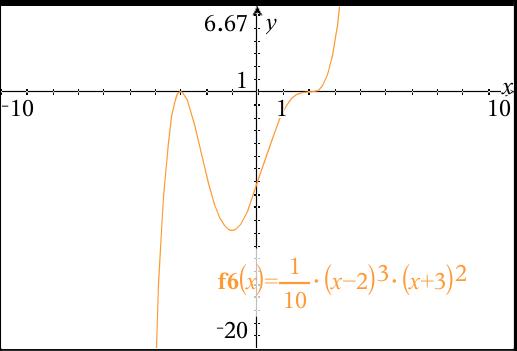
How do you use end behavior, zeros, y intercepts to sketch the graph of #g(x)=1/10(x-2)^3(x+3)^2#?
1 Answer
Apr 27, 2017
I like to take advantage of the factored form of the equation:
x - 2 means that x = 2 will be a zero
x+3 means that x = -3 will be a zero
Explanation:
The odd powered term
The even powered term
The total degree is 2 + 3 or 5. An odd total degree , with lead coefficient