How do you use Heron's formula to find the area of a triangle with sides of lengths #19 #, #14 #, and #14 #?
2 Answers
The area is
Explanation:
Heron's formula is shown here:
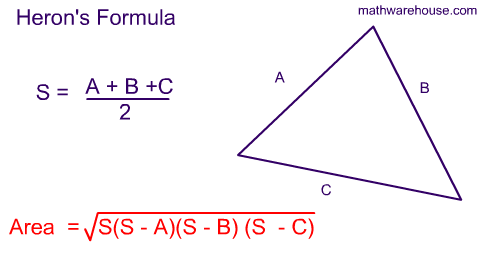
We know that the side lengths are
Simplify:
Now let's plug it into the formula for the area:
Now simplify:
Hope this helps!
Explanation:
The other answer perfectly answers the question asked. I will rephrase the question and then answer it to show some alternatives to Heron.
How do we find the area of a triangle with sides
That's an isosceles triangle, though we're not to depend on that for this problem.
Let's just start with the answer, which is called Archimedes' Theorem. It's a modern form of Heron.
Given triangle sides
Before we apply it, let's talk about it. We see it only depends on the squared sides, making it extra useful given vertex coordinates. (Two D coordinates can often be handled more expeditiously with the Shoelace Theorem.)
We also see the formula looks asymmetrical, but it must be symmetrical, giving the same result if we interchange
We plug in the numbers to get our answer.
That was is just one variant of Archimedes' Theorem/Heron's formula. The factored form is cool:
This form is probably the way to go with this problem:
Piece of cake. Both these alternatives avoid the fractions until the end, which makes them more more pleasant. The squared form is preferred given vertex coordinates.


