How do you use Heron's formula to find the area of a triangle with sides of lengths #29 #, #21 #, and #22 #?

Question

1996 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-27T01:21:18

#The Area = 230.04 units^2 #

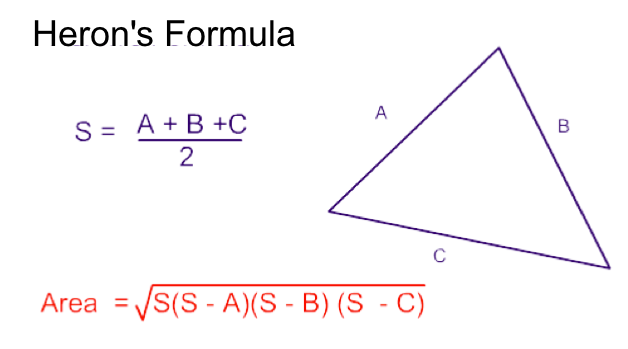
enter image source here

First we would find S which is the sum of the 3 sides divided by 2.

#S = (29 + 21 + 22)/2 # = #72/2# = 36

Then use Heron's Equation to calculate the area.

#Area = sqrt(S(S-A)(S-B)(S-C)) #

#Area = sqrt(36(36-29)(36-21)(36-22)) #

#Area = sqrt(33(7)(15)(14)) #

#Area = sqrt(52,920) #

#Area = 230.04 units^2 #