Question

How do you use Newton's method to find the approximate solution to the equation `tanx=e^x, 0<x<pi/2`?

Answer 1

`x=1.30633` to 6dp

Explanation:

Let `f(x) = tanx-e^x` Then our aim is to solve `f(x)=0` in the interval `0 lt x lt 1/2pi`

First let us look at the graphs:
graph{tanx-e^x [-1, 5, -15, 15]}

We can see there is one solution in the interval `0 < x < 1.57079 (=pi/2)`.

We can find the solution numerically, using Newton-Rhapson method

`f(x) = tanx-e^x => f'(x) = sec^2x-e^x`, and using the Newton-Rhapson method we use the following iterative sequence

`{ (x_0,=1), ( x_(n+1), = x_n - f(x_n)/(f'(x_n)) ) :}`

Then using excel working to 6dp we can tabulate the iterations as follows:

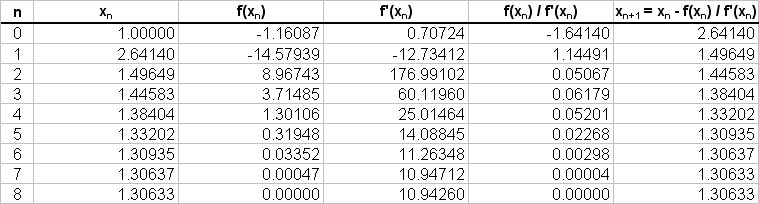
And we conclude that the remaining solution is `x=1.30633` to 6dp