Question

How do you use Newton's method to find the approximate solution to the equation `x^4=x+1,x>0`?

Answer 1

`x_1 = 1.2207440846`

Explanation:

We have:

`x^4 = x+1 => x^4-x-1=0`

Let:

`f(x) = x^4-x-1`

Our aim is to solve `f(x)=0`. First let us look at the graph:
graph{x^4-x-1 [-4, 4, -5, 10]}

We can see that there are two solutions; one solution in the interval `-1 lt x lt 0`, one in `0 lt x lt 2`. The root we find will depend upon our initial approximation `x_0`, and this value will require a little trial and error.

To find the solution numerically, using Newton-Rhapson method we use the following iterative sequence

`{ (x_1,=x_0), ( x_(n+1), = x_n - f(x_n)/(f'(x_n)) ) :}`

Therefore we need the derivative:

`\ \ \ \ \ \ \f(x) = x^4-x-1`
`:. f'(x) = 4x^3-1`

Then using excel working to 10dp we can tabulate the iterations as follows:

Initial Value `x_0=1`

Incidentally, we can also find the other solution `(x lt 0)`

Initial Value `x_0=0`

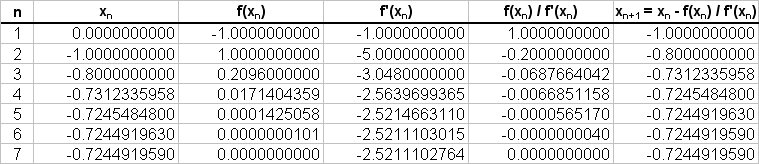
We could equally use a modern scientific graphing calculator as most new calculators have an " Ans " button that allows the last calculated result to be used as the input of an iterated expression.

And we conclude that the solution (to 10dp) are:

`x_1 = 1.2207440846`
`x_2 = -0.7244919590`