Question

How do you Use Simpson's rule with `n=8` to approximate the integral `int_0^pix^2*sin(x)dx`?

Answer 1

The answer is 5.86924686.

For any numerical approximation of a function, you always start with a table of values. For your problem, we have:

`a=0`
`b=pi`
`n=8`

So,

`Delta x=(b-a)/n=pi/8`
`x_i=a+i Delta x, i in {0, 1, ..., 8}`

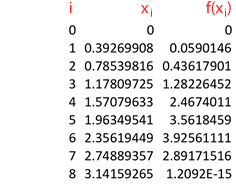
Now it is a matter of applying Simpson's Rule:

`int_0^pi x^2*sin x dx = int_0^pi f(x)dx ~~ (Delta x)/3(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+...+2f(x_6)+4f(x_7)+f(x_8))`

I'll skip the substitution of values because it's messy.
We get 5.86924686 as the approximation.

Using numerical integration on a calculator gets a value of 5.869604401 which means the approximation is good to 3 decimal places.

Notice the pattern of the coefficients for the sum is: 1, 4, 2, 4, ..., 2, 4, 1. This means that to use Simpson's Rule, we need an odd number of values or an even number of intervals; `n` is even.

Note that this integral can be solved using integration by parts twice to get an exact answer which is `pi^2-4`.