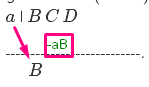The premise
given factor #(x-a)# to #f(x)=Bx^2+Cx+D#,
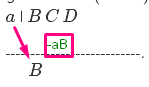
The pink arrow means multiply #a# by whatever the difference of the previous column's value was (it's subtraction).
You start out with taking #B# and putting it in the difference row, so the next column will be #C-aB#. The next column should be #D-a(C-aB)#, and so on. This applies to all polynomial equations.
Also, you CANNOT miss a term, so if you have something like #3x^5+8x^3-2x^2# you would have to write in 0s for the missing terms...
like this #\rightarrow3x^5+0x^4+8x^3-2x^2+0x-0#
Your result should have all the powers of #x# shifted down one degree, so a polynomial beginning with #x^5# would have a quotient beginning with #x^4#.
If the last column does not get you a #0# as the result, then it will be the remainder, which you put over the factor you divided by, #\frac(\text(remainder))(x-a)#
Actual calculation
#14x^2-34\leftrightarrow14x^2+0x-34#
dividing by #(x+4)#; from #(x-a)# form that means #a=-4#
So we have the synthetic division set up:
-4 | 14 0 -34
----.--------.------.
#\color{white}{abc}#14
-4 | 14 #\color{white}{a}# 0 #\color{white}{abc}#-34
#-##\color{white}{abc}#(-56) #\color{white}{a}#224
---.----------.----------.
#\color{white}{abc}#14#\color{white}{ab}#56#\color{white}{abc}#258
We get #14x-56+\frac{258}{x-4}#