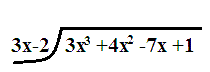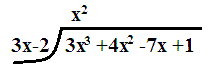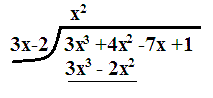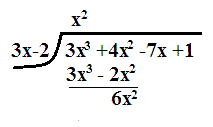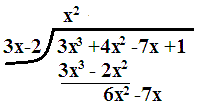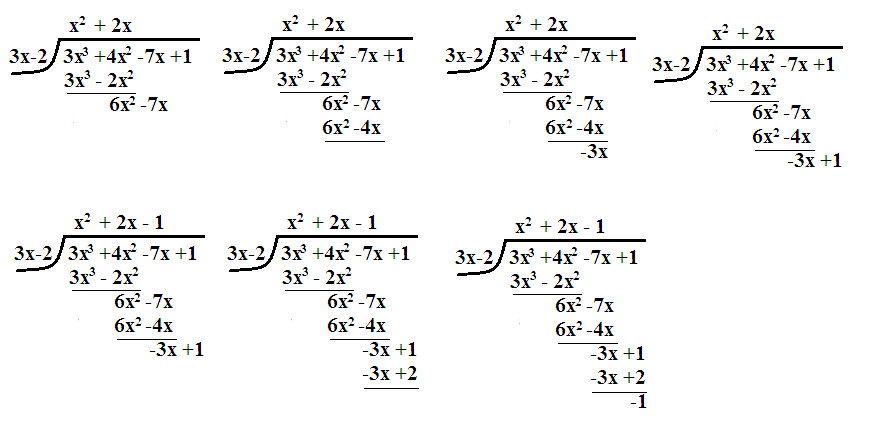Question

How do you use synthetic division to divide `3x^3+4x^2-7x+1` by `3x-2`?

Answer 1

`color(red)((3x^3 +4x^2-7x+6)/(3x-2) = x^2+2x-1-1/(3x-2))`

Explanation:

We use a slightly modified table when the coefficient of `x` does not equal `1`. Note the extra lines.

Step 1. Write only the coefficients of `x` in the dividend inside an upside-down division symbol.

`|3" "4" "-7" " " " "1`
`|color(white)(1)`
`stackrel("——————————————)`

Step 2. Put the divisor at the left.

`" "" "|3" "4" "-7" " " " "1`
`" "color(red)(2)color(white)(1)|`
`" "stackrel("——————————————)`

Step 3. Write the coefficient of `x` below the division line

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)2 " "" "4" "-2`
`" "stackrel("——————————————)`
`" "color(white)(1)|`
`color(red)(/3)color(white)(1)|`

Step 4. Drop the first coefficient of the dividend below the division symbol.

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)2 " "" "4" "-2`
`" "stackrel("——————————————)`
`" "color(white)(1)|color(red)(3)`
`/3color(white)(1)|`

Step 5. Divide the dropped value by the coefficient of `x` and place the result in the row below.

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)2 " "" "4" "-2`
`" "stackrel("——————————————)`
`" "" "|3`
`/3color(white)(1)|color(red)(1)`

Step 6. Multiply the result by the constant, and put the product in the next column.

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)color(red)(2)`
`" "stackrel("——————————————)`
`" "" "|3`
`/3color(white)(1)|1`

Step 7. Add down the column.

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)2`
`" "stackrel("——————————————)`
`" "" "|3" "color(red)(6)`
`/3color(white)(1)|1`

Step 8. Repeat Steps 5, 6, and 7 until you can go no farther.

`" "" "|3" "4" "-7" " " " "1`
`" "2|" "color(white)(1)2 " "" "4" "-2`
`" "stackrel("——————————————)`
`" "" "|3" "6" "-3" "color(red)(-1)`
`/3color(white)(1)|1" "2" "-1`

`(3x^3 +4x^2-7x+6)/(3x-2) = x^2+2x-1-1/(3x-2)`

Check:

`(3x-2)( x^2+2x-1-1/(3x-2)) = (3x-2)(x^2+2x-1)-1`

`= 3x^3+6x^2-3x-2x^2-4x+2-1 = 3x^3+4x^2-7x +1`

Answer 2

`(3x^3+4x^2-7x+1) div (3x-2)`
`color(white)("XXXX")` `= x^2+2x-1` `color(white)("XXXX")`Remainder: -1

Explanation:

Note that this is simply an alternate approach to Ernest Z's answer. Some people may find one approach easier to understand than the other.

Set up as standard long division:

`3x` " goes into " `3x^3` `color(white)("XXXX")` `rarr x^2` times:

Multiply `3x-2` by `x^2` and write the product below the line:

Subtract:

"Bring down" the `-7x`

`3x` " goes into " `6x^2` `color(white)("XXXX")` `rarr 2x` times
...and so on...

The Remainder of `(-1)` may be simply noted as a remainder or written as a fraction `(-1/(3x-2))_`