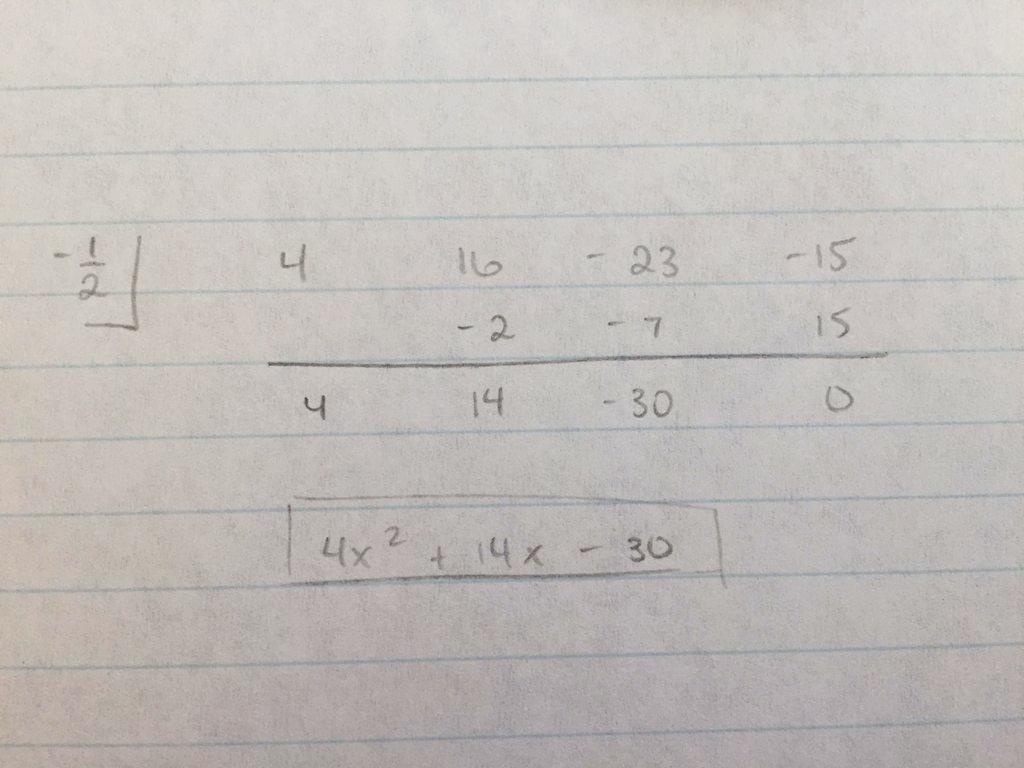First, determine your divisor, which will be the zero of the factor you're given. (It may or may not be a zero, but I'll discuss that later.) In this case, you are dividing by #x+1/2#, so the divisor is #-1/2#. I put this in the box on the left.
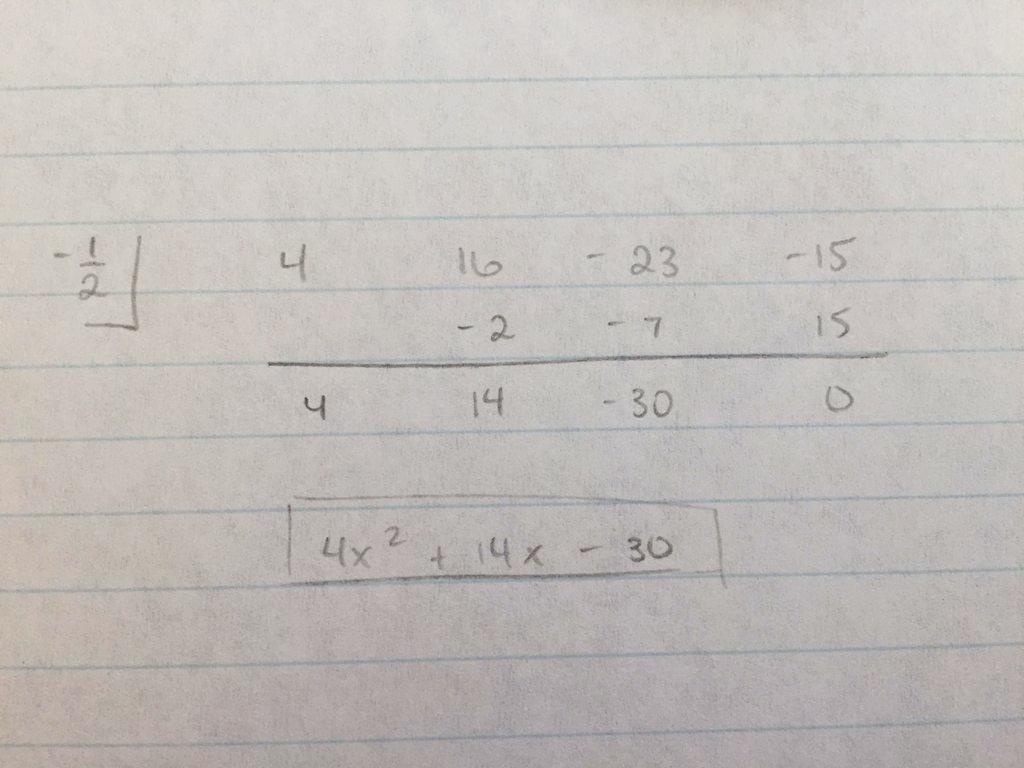
Next, bring down the coefficients of the dividend. Since the dividend is #4x^3 + 16x^2 - 23x - 15#, the coefficients are #4, 16, -23,# and #-15#.
Now, bring down the first coefficient, #4#, and place it below the line. Multiply #4# by the divisor, #-1/2#, to get #-2# and put it below the second coefficient, #16#. Now add #16# to #-2# to get #14#. Repeat these steps until you reach the last coefficient.
# 4 * -1/2 = -2 -> 16 + -2 = 14#
#14 * -1/2 = -7 -> -23 + -7 = -30#
#-30 * -1/2 = 15 -> -15 + 15 = 0#
In the end, we have four numbers: #4, 14, -30, 0#. These are the coefficients for the quotient. Since the problem asked us to divide #4x^3 + 16x^2 - 23x - 15# (cubic) by #x+1/2# (linear), the quotient will be quadratic. Thus, the degree of the first term will be #2#, the degree of the second term will be #1#, the degree of the third term will be #0# (the third term is a constant), and the last term will be the remainder.
#color(white)I#
Since the last term in this case is #0#, there is no remainder. This tells us that #x+1/2# is a factor of #4x^3 + 16x^2 - 23x - 15# because it divides evenly. If there was a remainder, the #x=-1/2# would not be a zero, and #x+1/2# would not be a factor.
In conclusion, our quotient is #color(blue)(4x^2 + 14x -30)#.