How do you use synthetic division to divide #( 4x^4 - 2x^2 - 1 ) / ( 2x - 1 )#?
1 Answer
The important thing is to remember to include missing powers of
Explanation:
Synthetic division of polynomials is similar to long division of numbers. There are other ways of laying it out but I like to write the coefficients of the dividend under the bar, those of the divisor to the left and start to write out each term of the quotient in turn above the bar, like so...
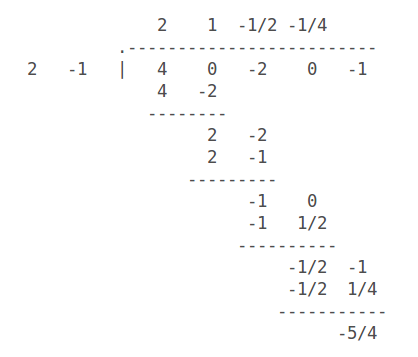
Choose each coefficient term in the quotient in order to match the leading term in your running remainder when multiplied by the divisor. For example, the first term
Having chosen a term for the dividend, write down the product of that and the divisor and subtract it from the dividend (or running remainder). Then bring down the next term of the dividend alongside it ready for the next choice of term for the quotient.
Continue in similar fashion until there are no more terms to bring down. The final running remainder is the remainder of the whole division.
In our case we find:
#4x^4+0x^3-2x^2+0x-1#
#= (2x-1)(2x^3+x^2-1/2x-1/4) - 5/4#
or if you prefer:
#(4x^4+0x^3-2x^2+0x-1)/(2x-1)#
#= (2x^3+x^2-1/2x-1/4) - (5/4)1/(2x-1)#

