How do you use synthetic division to divide #x^4-3x^3+3x^2-2x+3# by #x^2-3x+2#?
1 Answer
Jul 24, 2015
Explanation:
Step 1. Write only the coefficients of
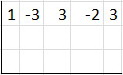
Step 2. Negate the coefficients in the divisor and put every coefficient but the first one diagonally at the left.
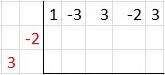
Step 3. Drop the first coefficient of the dividend below the division symbol.
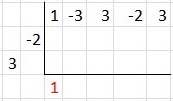
Step 4. Multiply the drop-down by the divisor, and put the result diagonally in the next columns.
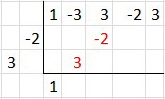
Step 5. Add down the column.
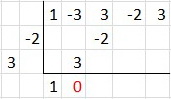
Step 6. Repeat Steps 4 and 5 until you would go past the entries at the top with the next diagonal.
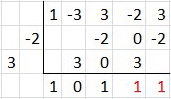
The quotient is
Check:

