How do you use synthetic division to divide #x^4 – 8x^3 + 16x^2 – 19# by #x-5#?
1 Answer
May 28, 2015
Synthetic Division is preformed in much the same manner as long division.
Note, however, the need to include all powers of
Hopefully the following image will demonstrate the process (because generating the series of step-by-step images is a lot of work)
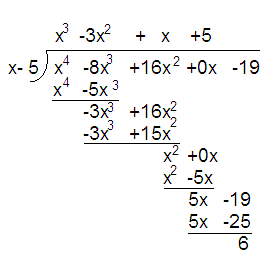
So
or
