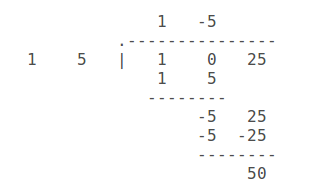#y^2+25 = y^2+0y+25# is represented by the sequence #1#, #0#, #25#.
#y+5# is represented by the sequence #1#, #5#.
Write out like long division of integers and proceed similarly:
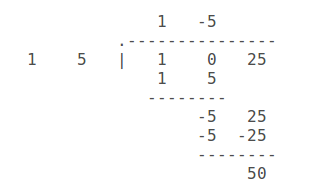
Write #1#, #0#, #25# under the bar as the dividend and #1#, #5# to the left as the divisor.
Identify #1# as the first term of the quotient - writing it above the bar - choosing it to cause the leading terms to match when the divisor is multiplied by it.
Write out #1 xx (1, 5)# under the dividend and subtract it to get the first term #-5# of a remainder.
Bring down the next term #25# of the dividend alongside it.
Identify #-5# as the second term of the quotient - writing above the bar - choosing it to cause the leading terms to match when the divisor is multiplied by it.
Write out #-5 xx (1, 5)# under the remainder and subtract it to get the remainder #50#.
We stop with this remainder since there are not enough terms remaining to make a sequence with enough terms to be divisible by the divisor.
So we have found:
#(y^2 + 25)/(y+5) = (y-5) + 50/(y+5)#
or if you prefer:
#y^2 + 25 = (y+5)(y-5) + 50#